COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
![]() Continuando nossa série de artigos/ vídeos sobre estruturas lógicas, aqui falaremos sobre tabela verdade.
Continuando nossa série de artigos/ vídeos sobre estruturas lógicas, aqui falaremos sobre tabela verdade.
Caso preferir, no vídeo abaixo tem esta postagem em áudio e vídeo
O assunto estruturas lógicas se divide em:
Proposições lógicas (lógica proposicional)
Tautologia, Contradição e Contingência
Tabela verdade:
Tabela verdade é uma tabela matemática usada no campo do raciocínio lógico, para verificar se uma proposição composta é válida.
Vamos agora aprender como se constrói uma tabela verdade.
Para sabermos quantas linhas terá nossa tabela verdade é só pegar o algarismo 2 e elevá-lo ao número de proposições simples.
Ex.: Duas proposições simples: 2² = 4
Três proposições simples : 2³ = 8
Vamos construir as duas:
Tabela verdade com duas proposições
Algarismo 2 elevado ao número de proposições que sabemos que são duas, então:
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
2² = 4
Temos então 4 linhas nesta tabela verdade.
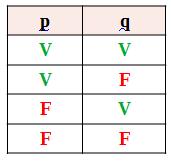
Na primeira coluna é só dividir o número de linhas por dois e colocar os valores lógicos verdadeiro (V) e falso (F)
São 4 linhas, então 4/2 = 2 Ficará duas verdadeiras e duas falsas colocadas simultaneamente
Na segunda coluna é só dividir o resultado da primeira por dois 2/2 = 1
Ficará uma verdadeira e uma falsa colocadas alternadamente
Tabela verdade com três proposições
É o mesmo processo:
Algarismo 2 elevado ao número de proposições que sabemos que são três, então:
2³ = 8
Temos então 8 linhas nesta tabela verdade.
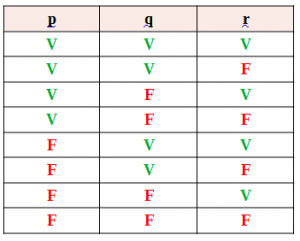
Na primeira coluna é só dividir o número de linhas por dois e colocar os valores lógicos verdadeiro (V) e falso (F).
São 8 linhas, então 8/2 = 4 Ficará quatro verdadeiras e quatro falsas colocadas alternadamente
Na segunda coluna é só dividir o resultado da primeira por dois 4/2 = 2 Ficará duas verdadeiras e duas falsas colocadas alternadamente
Na terceira coluna é só dividir o resultado da segunda por dois 2/2 = 1
Ficará uma verdadeira e uma falsa colocada alternadamente.
No próximo artigo/ vídeo falarei sobre:
Conectivos lógicos
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!


essa negação de r não seria F na primeira linha?
Oi Diego não sou especialista em raciocínio lógico e esta postagem foi baseada no site do professor Luiz Bianchi, deixarei suas dúvidas para os concurseiros que estão estudando confirmarem, mas caso você tenha certeza e dar seu parecer do por que posso verificar e corrigir a postagem se você estiver correto
Abraços e obrigado
q ^~ r da letra B ta correta?