COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
Em qual das possibilidades a situação foi descumprida?
Não é difícil concluir que na possibilidade 2, a situação foi descumprida. Você deve estar se perguntando sobre a possibilidade 3. Afinal, se não fez sol, como viajaram para a praia? Parece estranho, não? Na verdade, temos que tomar um certo cuidado, o pai só disse o que fariam se fizesse sol, mas não disse o que fariam se não fizesse sol. Esta é razão da condicional na linha 3 ser logicamente verdadeira. Temos que ter muita atenção, especialmente nesta parte. Esta é a parte que as pessoas, em geral, apresentam mais dificuldades de compreensão. Por este motivo vamos discutir um pouco mais sobre o assunto.
Utilizamos com frequência sentenças condicionais, como: “Se hoje chover, então vou ficar em casa”. Vamos ver as quatro possibilidades para esta situação:
- Choveu e fiquei em casa.
- Choveu e não fiquei em casa.
- Não choveu e fiquei em casa.
- Não choveu e não fiquei em casa.
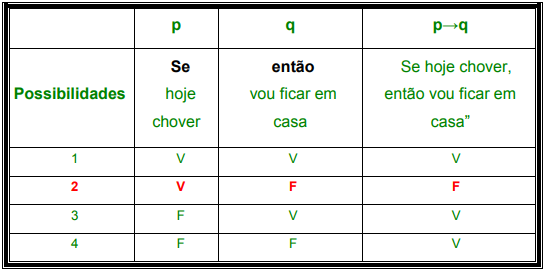
Caro aluno, é importantíssimo que você aprenda que na lógica matemática não nos preocupamos com qualquer relação de causa e efeito entre o antecedente e o consequente de uma implicação. O que há é uma relação entre os valores lógicos. Neste exemplo, ficou claro para você que na possibilidade 2, a situação foi descumprida; isto é, “choveu e não fiquei em casa” ? É provável que você tenha dúvidas com relação à possibilidade 3. Afinal, se não choveu, como fiquei em casa? Voltamos a dizer, sendo o antecedente (p) logicamente falso, não importa o valor lógico do consequente (q), pois o valor lógico da condicional será sempre verdadeiro!
Desta forma, releia o conceito:
A proposição condicional “se p então q” é uma proposição composta que só admite valor lógico falso no caso em que a proposição p é verdadeira e a proposição q é falsa, sendo verdade nas demais situações.
E qual é a importância da implicação?
O conceito de implicação é essencial para os diversos campos do conhecimento. Como exemplo, podemos citar as implicações lógicas de um discurso que remete a explicação ou demonstração de argumentos, e isto não é restrito à Matemática. É comum aparecerem declarações do tipo: “Sempre que isto ocorre, e, é verdadeiro, implica que aquilo também é verdadeiro”. Pense nas diversas áreas, tais como: Medicina, Direito, Engenharia, Educação, Propaganda e Marketing, Processamento de Dados e tantas outras áreas, que utilizam inúmeras implicações. Enfim vivemos imersos em um mundo de implicações lógicas! Pense a este respeito.
A implicação é muito importante na linguagem matemática porque aparece sistematicamente nos teoremas que constituem as teorias matemáticas. Um teorema é uma proposição do tipo p ⇒ q, onde p é uma proposição verdadeira na teoria em questão. Demonstrar um teorema não é mais do que provar que a proposição p ⇒ q é verdadeira e sendo p verdadeira, por hipótese, implica dizer que q é também verdadeira. Num teorema é comum chamarmos a proposição p de hipótese, é o antecedente da implicação p ⇒q. A proposição q, que é o consequente da implicação, é denominada de tese. As demonstrações de teoremas são essenciais para o desenvolvimento de habilidades e competências relacionadas à experimentação, observação e percepção, realização de conjecturas, desenvolvimento de argumentações convincentes, entre outras.
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!

O símbolo P⇒ Q (P implica Q) representa a implicação lógica. Observe neste conceito que aparecem dois símbolos matemáticos → e ⇒. Vamos diferenciá-los?
Diferenciação dos símbolos → e ⇒
- O símbolo → (p → q) Lê-se: se p….. então q representa uma operação matemática entre as proposições p e q que tem como resultado a proposição p → q, com valor lógico V ou F.
- O símbolo ⇒ ( P⇒ Q) Lê-se: P implica Q representa a não ocorrência de VF na tabela-verdade de P → Q, ou ainda que o valor lógico da condicional P → Q será sempre V, ou então que P → Q é uma tautologia.
Você já deve ter se familiarizado com o primeiro (símbolo →), pois fizemos uso dele em vários exemplos envolvendo a operação lógica da condicional em que podíamos fazer um julgamento (verdadeiro ou falso), já o segundo (símbolo ⇒) passaremos a ver agora com mais detalhes. Tenha sempre em mente que o símbolo ⇒ representa uma implicação, cuja condicional será sempre tautológica, isto é, será sempre logicamente verdadeira. Vamos agora ver alguns exemplos e verificar a implicação lógica indicada em cada caso.
Exemplos:

Vamos comprovar isto para o 1ª exemplo dado. p ^ q ⇒ p
Considere a situação:
p: Marina Silva vencerá as eleições para a Presidência do Brasil.
q: A taxa de desemprego cairá nos próximos três anos.
p ^ q: Marina Silva vencerá as eleições para a Presidência do Brasil e a taxa de desemprego cairá nos próximos três anos.
Vamos agora verificar como ficam os possíveis valores lógicos das proposições:

Relembrando: Você está lembrado que a proposição composta da conjunção p ^ q (p e q) somente será verdadeira quando as proposições p e q forem verdadeiras.
Perceba que quando p ^ q é verdadeira (1ª possibilidade, veja o quadro acima), p é verdadeira também, logo dizemos que p ^ q implica p e, tem a seguinte notação: p ^ q ⇒ p. E mais, se você fizer a condicional (p ^ q) → p, ela será sempre verdadeira, ou seja uma tautologia.
2º exemplo: p ⇒ q → p Vamos verificar esta implicação.
Continua na parte 3
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!

