COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
 Conceito de Função:
Conceito de Função:
O conceito básico é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função.
De um modo geral, dados dois conjuntos A e B, e uma relação entre eles, dizemos que essa relação é uma função de A em B se e somente se, para todo x A existe um único y B de modo que x se relacione com y
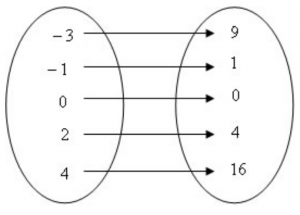
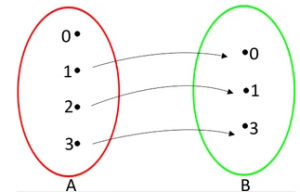
Não é função
Fonte: Só matemática
Função afim ou polinomial do primeiro grau
Para saber se uma função é polinomial do primeiro grau, devemos observar o maior grau da variável x (termo desconhecido), que sempre deve ser igual a 1. Nessa função, o gráfico é uma reta. Além disso, ela possui: domínio x, imagem f(x) e coeficientes a e b.
Fórmula geral da função afim ou polinomial do primeiro grau
f(x) = ax + b
x = domínio
f(x) = imagem
a = coeficiente
b = coeficiente
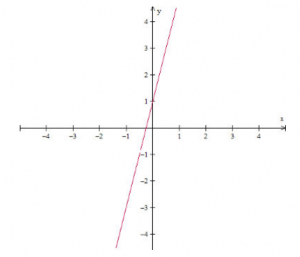
Exemplo de gráfico da função polinomial do primeiro grau: f(x) = 4x + 1
Função quadrática ou polinomial do segundo grau
Identificamos que uma função é do segundo grau quando o maior expoente que acompanha a variável x (termo desconhecido) é 2. O gráfico da função polinomial do segundo grau sempre será uma parábola. A sua concavidade muda de acordo com o valor do coeficiente a. Sendo assim, se a é positivo, a concavidade é para cima e, se for negativo, é para baixo.
Fórmula geral da função quadrática ou polinomial do segundo grau
f(x) = ax2 + bx + c
x = domínio
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
f(x) = imagem
a = coeficiente que determina a concavidade da parábola.
b = coeficiente.
c = coeficiente.
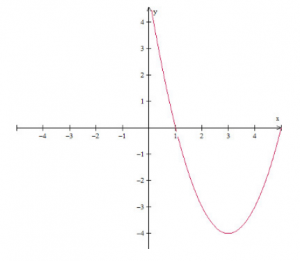
Exemplo de gráfico da função polinomial do segundo grau: f(x) = x2 – 6x + 5
Função exponencial
Uma função será considerada exponencial quando a variável x estiver no expoente em relação à base de um termo numérico ou algébrico. Caso esse termo seja maior que 1, o gráfico da função exponencial é crescente. Mas se o termo for um número entre 0 e 1, o gráfico da função exponencial é decrescente.
Fórmula geral da função exponencial
f(x) = ax
a > 1 ou 0 < a < 1
x = domínio
f(x) = imagem
a = Termo numérico ou algébrico
Exemplo de gráfico da função exponencial crescente: f(x) = (2)x, para a = 2
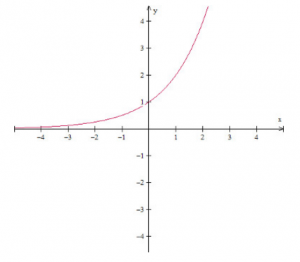
Exemplo de gráfico da função exponencial decrescente: f(x) = (1/2)x para a = ½

Função logarítmica
Na função logarítmica, o domínio é o conjunto dos números reais maiores que zero e o contradomínio é o conjunto dos elementos dependentes da função, sendo todos números reais.
Fórmula geral da função logarítmica
f(x) = loga x
a = base do logaritmo
f(x) = Imagem/ logaritmando
x = Domínio/ logaritmo
Exemplo de gráfico da função logarítmica: f(x) = log10 (5x – 6)
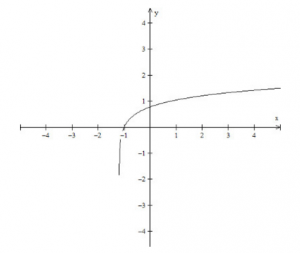
Fonte: Mundo Educação
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!

