Problemas e inequações do 2º grau
Uma inequação do 2° grau na incógnita x é uma expressão do 2° grau que pode ser escrita numa das seguintes formas:
ax² + bx + c > 0;
ax² + bx + c < 0;
ax² + bx + c ≥ 0;
ax² + bx + c ≤ 0.
onde a, b e c pertencem ao conjunto dos números reais e a ≠ 0.
Produtos notáveis
Quando algumas expressões algébricas possuem características comuns ao serem resolvidas, são chamadas de produtos notáveis, pois respeitam uma lógica matemática. Esses produtos podem ser resolvidos através da multiplicação distributiva ou por uma fórmula.
Através da fórmula, reduzimos os cálculos e o tempo de resolução do exercício, propiciando uma maior rapidez na resolução das questões (uma praticidade bastante almejada).
Para alguns, a memorização de fórmulas é um problema, por isso, sempre que a memória falhar, não se preocupe, aplique a multiplicação distributiva que você obterá o mesmo resultado, afinal de contas, essas fórmulas foram determinadas através da realização dessa técnica.
Observe nos produtos notáveis abaixo:
Equações
Na matemática, uma equação é uma igualdade envolvendo uma ou mais incógnitas (valores desconhecidos).
São exemplos de equações as seguintes igualdades:
x+8=15
x³-9x²-7=4
3sen(x)+25cos(x)=18
3x4-x3+5x²-34x+1211=0
Nesses exemplos, as letras x e y são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.
A equação x+8=15 pode ser interpretada como uma pergunta: “qual o número que somado com 8 dá 15?”. Não é necessário nenhum método ou fórmula para encontrar o valor de x nesse caso: basta pensar um pouco para se chegar ao resultado x=7.
Resolver uma equação é encontrar todos os valores possíveis para a incógnita que tornem a igualdade verdadeira. As equações mostradas nos exemplos acima podem ser interpretadas e resolvidas facilmente: o número que subtraído de 10 é igual a 4 é m=6; o número que, ao ser multiplicado por 3, resulta em 18 é y=6.
Uma solução da equação pode ser compreendida como a raiz de uma função.
Algumas equações matemáticas descrevem, na verdade, identidades matemáticas, isto é, afirmações que são verdadeiras para todos os valores de x, como nos exemplos:
x(x+5)=x²+5x
sen²x+cos²x=1
Entretanto, uma equação pode ter apenas alguns valores para os quais ela se torna verdadeira. Nesse caso, ela deve ser resolvida para se encontrar os valores possíveis para as incógnitas. Por exemplo, considere a equação:
X²-3x=0.
Ela é satisfeita para exatamente dois valores de x, a saber, x=0} x=0 e x=3.
Em geral, os matemáticos reservam a palavra equação exclusivamente para igualdades que não são identidades. A distinção entre esses dois conceitos pode ser bastante sutil. Por exemplo:
(x+1)²=x²+2x+1
é uma identidade, mas:
(x+1)²=2x²+x+1
é uma equação cujas soluções são x = 0 e x=1.
Em geral, é possível perceber se se trata de uma identidade ou de uma equação pelo contexto em que a igualdade se encontra. Em alguns casos, na identidade, o sinal de igualdade (=) é trocado pelo sinal (≡).
Fonte: Wikipédia
Veja também: Equações do 1º grau e Equações do 2º grau
E você, qual o concurso você vai fazer? Deixe um comentário para mim, pois posso fazer postagens direcionadas para ele e te ajudar mais. Aproveita também para inscrever seu e-mail para receber conteúdos todos os dias.
Dica: Para você que não esta encontrando o conteúdo que precisa ou prefere estudar por apostilas dá uma olhada no site Apostilas Opção, lá eles tem praticamente todas as apostilas atualizadas de todos os concursos abertos. Caso queira saber por que indico as Apostilas Opção clique aqui!
Ponto material e corpo extenso
Cinemática – É a ciência que estuda o movimento dos corpos independentemente das causas deste. Na cinemática por exemplo estudaremos a aceleração, a velocidade e a posição de determinado objeto após certo tempo de movimento.
Para aprofundar mais sobre os conceitos de cinemática veja também esta postagem; Conceitos de Cinemática
Ponto material
Considerando um navio fazendo uma viajem do Rio de Janeiro até o continente africano, podemos verificar que as dimensões do navio pouco importam em relação a distância que ele irá percorrer. Neste caso, dizemos que o navio é um ponto material.
Um ponto material, portanto, é todo corpo cujas dimensões não interferem no estudo de um determinado fenômeno.
Corpo extenso
Se porventura a situação que considerarmos ser a de navio entrar no porto, suas dimensões não poderão ser desprezadas em relação ao tamanho do porto. Neste caso denominamos o navio de corpo extenso.
Corpo extenso é todo corpo cujas as dimensões interferem no estudo de determinado fenômeno.
Fonte: S.O.S. Aprender
Expressões literais e algébricas
Expressões algébricas são expressões matemáticas que apresentam letras e podem conter números, são também denominadas expressões literais. As letras constituem a parte variável das expressões, pois elas podem assumir qualquer valor numérico. No passado as letras foram pouco utilizadas na representação de números desconhecidos, atualmente as letras associadas a números constituem a base da álgebra e contribui de forma eficiente na resolução de várias situações matemáticas. Veja alguns exemplos de expressões algébricas:
2x – 5
3a + 2y
x² + 7x
5 + x – (5x – 2)
10y – 10x
a² – 2ab + b²
Simplificação de Expressões Algébricas
►y + y + y = 3y —— pois os monômios são semelhantes (as letras são iguais e os seus expoentes também.
►m – 7m = -6m —— pois os monômios são semelhantes (as letras são iguais e os seus expoentes também.
►5 . (x + 2) – 8 . x ——– utilizando a propriedade distributiva
5x + 10 – 8x———- 5x e 8x são monômios semelhantes
-3x + 10———como -3x e 10 não são semelhantes então não pode somar.
Concluímos que:
5 . (x + 2) – 8 . x = -3x + 10
Prioridade das operações numa expressão algébrica
Nas operações em uma expressão algébrica, devemos obedecer a seguinte ordem:
Potenciação ou Radiciação
Multiplicação ou Divisão
Adição ou Subtração
Observações quanto à prioridade:
Antes de cada uma das três operações citadas, deve-se realizar a operação que estiver dentro dos parênteses, colchetes ou chaves.
A multiplicação pode ser indicada por × ou por um ponto · ou às vezes sem sinal, desde que fique clara a intenção da expressão.
Muitas vezes devemos utilizar parênteses quando substituímos variáveis por valores negativos.
Exemplos:
Consideremos P=2A+10 e tomemos A=5. Assim
P = 2.5+10 = 10+10 = 20
Aqui A é a variável da expressão, 5 é o valor numérico da variável e 20 é o valor numérico da expressão indicada por P. Observe que ao mudar o valor de A para 9, teremos:
A = 2.9 + 10 = 18 + 10 = 28
Se A=9, o valor numérico de P=2A+10 é igual a 28.
Seja X=4A+2+B-7 e tomemos A=5 e B=7. Assim:
X = 4.5+2+7-7 = 20+2-0 = 22
Se A=5 e B=7, o valor numérico de X=4A+2+B-7, muda para 22.
Seja Y=18-C+9+D+8C, onde C= -2 e D=1. Então:
Y = 18-(-2)+9+1+8(-2) = 18+2+9+1-16 = 30-16 = 14
Se C=-2 e D=1, o valor numérico de Y=18-C+9+D+8C, é 14.
Conclusão: O valor numérico de uma expressão algébrica é o valor obtido na expressão quando substituímos a variável por um valor numérico.
Fontes: Brasil escola, Mundo Educação e Sercomtel
No final da postagem tem várias videoaulas para você assistir.
Dica: Estou atualizando o Conteúdo Programático completo do ENEM e além disso, para você que não esta encontrando todo o conteúdo do Enem ou prefere estudar por apostilas dá uma olhada nesta apostilas para ENEM do site Apostilas Opção é bem interessante.
Bons estudos!
Átomos: Semelhanças atômicas, distribuição eletrônica e modelos atômicos.
Se analisarmos o número atômico (Z), o número de nêutrons (N) e o número de massa (A) de átomos diferentes, será possível identificar e formar conjuntos de átomos com algumas similaridades. Esta propriedade dos átomos recebe o nome de semelhança atômica.
Isótopos: átomos pertencentes a um mesmo elemento químico, portanto possuem números atômicos iguais. Os isótopos se diferenciam com relação ao número de massa, acompanhe os exemplos:
O elemento químico Magnésio (Mg) possui os seguintes isótopos:
12Mg24 (presente na natureza com a porcentagem de 78,9%)
12Mg25 (presente na natureza com a porcentagem de 10,0%)
12Mg26 (presente na natureza com a porcentagem de 11,1%)
Os isótopos de hidrogênio recebem nomenclatura própria, veja:
Átomos: Número atômico, número de massa, isótopos, massa atômica
No final da postagem tem uma videoaula bem interessante, vale a pena conferir.
Dica: Estou atualizando o Conteúdo Programático completo do ENEM e além disso, para você que não esta encontrando todo o conteúdo do Enem ou prefere estudar por apostilas dá uma olhada nesta apostilas para ENEM do site Apostilas Opção é bem interessante.
Bons estudos!
Átomos: Número atômico, número de massa, isótopos, massa atômica
Os modelos atômicos propostos indicam que os átomos diferem entre si pelo número de prótons, nêutrons e elétrons que contêm. Para identificar o número dessas partículas, são determinados o número de massa e o número atômico.
As massas atômicas são determinadas por comparação das massas dos átomos com um padrão de massas que equivale a 1/12 da massa do átomo de carbono. O valor numérico da massa atômica é muito próximo do valor do número de massa.
O número de massa e o número atômico
Um átomo pode ser definido mediante dois números:
O número atômico, cujo símbolo é Z, é o número de prótons que tem um átomo. Como o átomo isolado é neutro, o número de prótons coincide com o número de elétrons.
Z = número de prótons = número de elétrons (para um átomo neutro)
O número de massa, cujo símbolo é A, é o número de partículas que tem um átomo em seu núcleo. É a soma de prótons e nêutrons.
A = número de massa = número de prótons + número de nêutrons
A = Z + N
O que realmente identifica o elemento a que pertence o átomo é o número atômico (Z). O valor de A é útil, mas não identifica de que elemento é o átomo em questão.
Representação abreviada dos átomos
Fenômenos físicos e químicos:
Primeiramente vamos definir o que é um fenômeno:
Sempre que a matéria sofre uma transformação qualquer, dizemos que ela sofreu um fenômeno, que pode ser físico ou químico.
Exemplo: Quando pegamos uma folha de papel e simplesmente a rasgamos, modificamos seu formato e tamanho, mas ainda temos o papel(fenômeno físico). Porém, se essa folha for queimada, teremos modificação na sua composição(fenômeno químico).
Vamos aprofundar mais:
Sólido – gás
Para separarmos sólidos de gases, em uma mistura heterogênea, podemos aplicar os seguintes processos:
Filtração: A simples filtração também presta-se muito bem na separação entre gases e sólidos, onde a mistura passa através de um filtro, no qual o sólido fica retido. Esse processo é muito utilizado nas indústrias, principalmente para evitar o lançamento de partículas sólidas na atmosfera. A filtração é também usada cotidianamente nos aspiradores de pó, onde o sólido é retido (poeira) à medida que o ar é aspirado.
Mudanças de estado
A matéria pode apresentar-se em qualquer estado físico, dependendo dos fatores pressão e temperatura. Assim, de modo geral, o aumento de temperatura e a redução de pressão favorecem o estado gasoso, e pode-se dizer que o inverso favorece ao estado sólido. As transformações de estado físico da matéria apresentam denominações características, como se pode ver abaixo:
a) FUSÃO: é a passagem do estado sólido para o estado líquido. Isto se verifica quando o corpo sólido recebe calor, o que provoca uma elevação na sua temperatura até o ponto em que a agitação das átomos passa a ser tanta que a estrutura deixa de ser cristalina e passam a ter uma movimentação maior, caracterizando o líquido.
Durante a fusão a temperatura permanece constante, conforme podemos constatar ao retirarmos um bloco de gelo do congelador e colocar em um prato.
Temperatura de fusão: É a temperatura na qual ocorre a passagem do estado sólido para o líquido.
b) VAPORIZAÇÃO: representa a passagem do estado líquido para o estado gasoso. A temperatura na qual ocorre recebe o nome de Ponto de Ebulição. Uma vaporização pode ocorrer de três modos distintos:
CALEFAÇÃO: passagem do estado líquido para o gasoso de modo muito rápido, quase instantâneo. Por exemplo, gotas de água sendo derramadas em uma chapa metálica aquecida.
EBULIÇÃO: passagem do estado líquido para o estado gasoso por meio de aquecimento direto, envolvendo todo o líquido. Por exemplo, o aquecimento da água em uma panela ao fogão.
Temperatura de Ebulição: Ocorre à uma determinada temperatura, característica de cada líquido, chamada.
Cada substância possui uma determinada temperatura de ebulição e a mesma permanece constante enquanto se verifica o processo. Ex: a água entra em ebulição à 100ºC e permanece nessa temperatura enquanto estiver fervendo.
EVAPORAÇÃO: passagem do estado líquido para o estado gasoso que envolve apenas a superfície do líquido. Por exemplo, a secagem de roupas em um varal.
c) LIQUEFAÇÃO ou CONDENSAÇÃO: representa a passagem do estado gasoso para o estado líquido. Isto se verifica quando se retira calor de uma substância que está em ebulição.
Por exemplo, a umidade externa de um frasco metálico ao ser exposto a uma temperatura relativamente elevada.
d) SOLIDIFICAÇÃO: representa a passagem do estado líquido para o estado sólido. Por exemplo, o congelamento da água em uma forma de gelo levada ao refrigerador.
Isto se verifica quando se retira calor do corpo líquido, o que provoca uma diminuição na sua temperatura até o ponto em que a agitação dos átomos diminui tanto que passam a vibrar segundo uma estrutura cristalina.
Temperatura de solidificação: É a temperatura na qual ocorre a passagem do estado líquido para o sólido.
Durante a solidificação a temperatura permanece constante.
e) SUBLIMAÇÃO: representa a passagem do estado sólido para o estado gasoso ou o processo inverso, sem passagem pelo estado líquido. Por exemplo, a sublimação do gás carbônico sólido, conhecido por gelo seco, em exposição à temperatura ambiente.
f) CRISTALIZAÇÃO: É a passagem do estado gasoso direto para o estado sólido, sem passar pelo estado líquido. Ex: se aquecermos iodo cristalino o mesmo irá evaporar. Colocando-se uma superfície fria logo acima da evaporação notaremos que o mesmo se liga a superfície na forma de pequenos cristais.
Fonte: Infoescola e Cola da web
Estados físicos de materiais
A matéria é composta por pequenas partículas e, de acordo com o maior ou menor grau de agregação entre elas, pode ser encontrada em três estados: sólido, líquido e gasoso.
O que determina o estado em que a matéria se encontra é a proximidade das partículas que a constitui. Essa característica obedece a fatores como:
Força de Coesão: faz com que as moléculas se aproximem umas das outras.
Força de Repulsão: faz com que as moléculas se afastem umas das outras.
Esses estados de agregação da matéria também são chamados de estados físicos da matéria.
Importante: O volume, a densidade e a forma de um composto, podem variar de acordo com a temperatura.
Estado Sólido: as moléculas da matéria se encontram muito próximas, sendo assim possuem forma fixa, volume fixo e não sofrem compressão. As forças de atração (coesão) predominam neste caso. Um exemplo é um cubo de gelo, as moléculas estão muito próximas e não se deslocam ao menos que passe por um aquecimento.
Estado Líquido: Aqui as moléculas estão mais afastadas do que no estado sólido e as forças de repulsão são um pouco maiores. Os elementos que se encontram nesse estado, possuem forma variada, mas volume constante. Além destas características, possui facilidade de escoamento e adquirem a forma do recipiente que os contém.
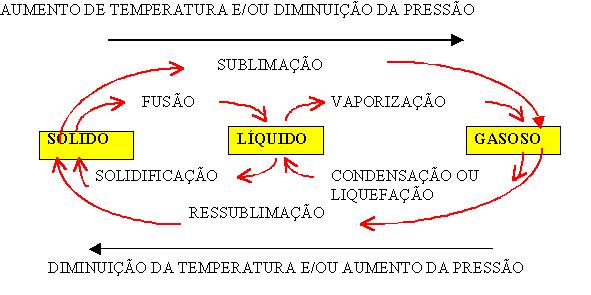
.jpg)
Estado Gasoso: a movimentação das moléculas nesse estado é bem maior que no estado líquido ou sólido. Se variarmos a pressão exercida sobre um gás podemos aumentar ou diminuir o volume dele, sendo assim, pode-se dizer que sofre compressão e expansão facilmente. Os elementos gasosos tomam a forma do recipiente que os contém.
Essas características obedecem a fatores como a Força de Coesão (faz com que as moléculas se aproximem umas das outras) e a Força de Repulsão (as moléculas se afastem umas das outras). No estado gasoso a Força de Repulsão predomina, enquanto que no estado sólido é a Força de Coesão.
Assim, quando uma substância muda de estado físico sofre alterações nas suas características microscópicas (arranjo das partículas) e macroscópicas (volume, forma), sendo que a composição continua a mesma.
Estado Plasma: Somente ocorre em condições altíssimas de temperatura, como no núcleo do Sol. Lá, os átomos de hélio ficam a uma temperatura e pressão muito altas, fazendo com que os seus elétrons sejam desprendidos de seus átomos.
FONTES: Brasil escola e Info escola
EXERCÍCIOS
(UEL) Três ciclistas percorrem um circuito saindo todos ao mesmo tempo, do mesmo ponto, e com o mesmo sentido. O primeiro faz o percurso em 40 s, o segundo em 36 s e o terceiro em 30 s. Com base nessas informações, depois de quanto tempo os três ciclistas se reencontrarão novamente no ponto de partida, pela primeira vez, e quantas voltas terá dado o primeiro, o segundo e o terceiro ciclistas, respectivamente?
(A) 5 minutos, 10 voltas, 11 voltas e 13 voltas.
(B) 6 minutos, 9 voltas, 10 voltas e 12 voltas.
(C) 7 minutos, 10 voltas, 11 voltas e 12 voltas.
(D) 8 minutos, 8 voltas, 9 voltas e 10 voltas.
(E) 9 minutos, 9 voltas, 11 voltas e 12 voltas.
MÁXIMO DIVISOR COMUM (MDC)
O máximo divisor comum, ou MDC, de dois ou mais números inteiros é o maior divisor inteiro comum a todos eles. Por exemplo, o m.d.c. de 16 e 36 é o 4, e denotamos isso por MDC 16, 36 = 8. Já o MDC de 30, 54 e 72 é o 6, o que é denotado por MDC 30, 54, 72 = 6.
Regra geral para calcular o MDC de dois ou mais números. O procedimento geral para o cálculo do MDC, como no caso do MMC, envolve a decomposição primária de cada número.
Propriedade fundamental do MDC. Todo divisor comum de dois ou mais números inteiros é divisor do MDC destes números.
Exemplo: 3 é divisor comum de 30, 36 e 72. Observe que 3 também é divisor de 6, o MDC destes três números.
O máximo divisor comum (mdc) entre dois números naturais é obtido a partir da interseção dos divisores naturais, escolhendo-se o maior.
O mdc pode ser calculado pelo produto dos fatores primos que são comuns tomando-se sempre o de menor expoente.
Exemplo: 120 e 36
120 2 36 2
60 2 18 2
30 2 9 3
15 3 3 3
5 5 1 22.32
1 23.3.5
m.d.c ( 120, 36) = 22.3 = 12
O m.d.c também pode ser calculado pela decomposição simultânea em fatores primos, tomando apenas os fatores que dividem simultaneamente.
120 – 36 2 ( * )
60 – 18 2 ( * )
30 – 9 2
15 – 9 3 ( * )
5 – 3 3
5 – 1 5
1 – 1 22.3 = 12
Coloquei duas explicações que talvez você compreenda melhor, devido aos estilos serem um pouco diferentes.
O mínimo múltiplo comum, ou MMC, de dois ou mais números inteiros é o menor múltiplo inteiro positivo comum a todos eles. Por exemplo, o MMC de 6 e 8 é o 24, e denotamos isso por mmc 6, 8 = 24 Já o MMC de 5, 6 e 8 é o 120, o que é denotado por MMC 5, 6, 8 = 120.
Células Eucariótica
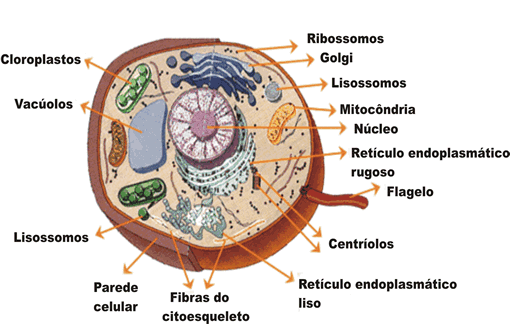Já as células eucarióticas, possuem maior tamanho e complexidade, a começar pelo núcleo individualizado, envolvido pela carioteca. Seu citoplasma é interconectado por uma rede de tubos e canais membranosos e é onde, além de ribossomos, também são encontradas mitocôndrias, retículo endoplasmático granuloso e não granuloso, complexo golgiense, lisossomos, peroxissomos, centríolos, dentre outras organelas.
Exemplos de indivíduos eucariotas: animais, vegetais, fungos e protozoários.
As células eucariontes ou eucarióticas, também chamadas de eucélulas, são mais complexas que as procariontes. Possuem membrana nuclear individualizada e vários tipos de organelas. A maioria dos animais e plantas a que estamos habituados são dotados deste tipo de células.
