Questão de Raciocínio lógico 8 …às letras da palavra JUNCO é igual a
Resolução no vídeo:
Ano: 2023 Banca: FUNCERN Órgão: Prefeitura de Junco do Seridó – PB Cargo: Nutricionista Escolar
Questão de Raciocínio lógico 7
Solução no vídeo
Ano: 2023 Banca: IDESG Órgão: Prefeitura de Vila Valério – ES Cargo: Fiscal de Obras
Sabendo que a sequência: 1; 1; 2; 3; 5; 8; 13…? Questão de raciocínio lógico
Raciocínio lógico com figuras 7 – Ano 2023
Solução no vídeo
Ano: 2023 Banca: Instituto Consulplan Órgão: Prefeitura de Orlândia – SP Cargo: Bombeiro Municipal
Observe a sequência lógica:
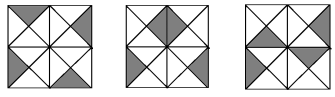
Questão raciocínio lógico 5
QUESTÃO 1
Ano: 2023 Banca: OBJETIVA Órgão: Prefeitura de Nova Bréscia – RS Cargo: Operador de Máquinas
Analise a sequência a seguir:
Resolução no vídeo:
Questão de raciocínio lógico figura 5
Resolução da questão no vídeo:
Ano: 2021 Banca: FUNDEP (Gestão de Concursos) Órgão: Prefeitura de Itapecerica da Serra – SP
Questão de raciocínio lógico figura 5
Resolução da questão no vídeo:
Ano: 2022 Banca: MetroCapital Soluções Órgão: Prefeitura de Nova Odessa – SP Cargo: Contador
Disciplina: Raciocínio lógico Assunto: Problemas lógicos com dados, figuras e palitos
Questão de raciocínio lógico figura 4
Resolução da questão no vídeo
Ano: 2022 Banca: MetroCapital Soluções Órgão: Prefeitura de Nova Odessa – SP Cargo: Agente Comunitário de Saúde
Questão de raciocínio lógico sequência 3
Resolução no vídeo abaixo:
Ano: 2022 Banca: FURG Órgão: FURG Prova: FURG – 2022 – FURG – Assistente em Administração
Ano: 2022 Banca: IPEFAE Órgão: Câmara de Espírito Santo do Pinhal – SP Cargo: Assessor Jurídico
Disciplina: Raciocínio lógico Assunto: Problemas lógicos com dados, figuras e palitos
Identificando a regularidade da sequência figural abaixo, podemos concluir que o próximo elemento da sequência é:
Questão e solução no vídeo
Questão de raciocínio lógico – Figuras 1
RESOLUÇÃO NO VÍDEO ABAIXO:
Ano: 2022 Banca: CESPE / CEBRASPE Órgão: POLITEC – RO Cargo: Perito Criminal
Disciplina: Raciocínio lógico Assunto: Problemas lógicos com dados, figuras e palitos
Questão de raciocínio lógico – Sequência numérica
(TRT 9ª Região – Auxiliar Judiciário/2004)
Observe atentamente a tabela:
De acordo com o padrão estabelecido, o espaço em branco na última coluna da tabela deve ser preenchido com o número:
a) 2 b) 3 c) 4 d) 5 e) 6
RESPOSTA NO VÍDEO
Diagramas lógicos – Diagrama de Venn
Leia/ assista o vídeo até o final que resolverei 2 questões de concursos para você entender melhor
Os diagramas lógicos são usados para representar as proposições de um raciocínio lógico.
Se preferir, no vídeo abaixo tem a postagem em áudio e vídeo:
As questões de raciocínio lógico que usam os diagramas utilizam os quantificadores:
QUESTÃO 22 PRF 2019 Raciocínio Lógico
Uma unidade da PRF interceptou, durante vários meses, lotes de mercadorias vendidas por uma empresa com a emissão de notas fiscais falsas. A sequência dos números das notas fiscais apreendidas, ordenados pela data de interceptação, é a seguinte: 25, 75, 50, 150, 100, 300, 200, 600, 400, 1.200, 800, ….
Tendo como referência essa situação hipotética, julgue os itens seguintes, considerando que a sequência dos números das notas fiscais apreendidas segue o padrão apresentado.
A partir do padrão da sequência, infere-se que o 12.º termo é o número 1.600.
( ) CERTO
( ) ERRADO
Solução no vídeo