COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
Problemas e inequações do 2º grau
Uma inequação do 2° grau na incógnita x é uma expressão do 2° grau que pode ser escrita numa das seguintes formas:
ax² + bx + c > 0;
ax² + bx + c < 0;
ax² + bx + c ≥ 0;
ax² + bx + c ≤ 0.
onde a, b e c pertencem ao conjunto dos números reais e a ≠ 0.
Significado dos sinais:
>: maior que
<: menor que
≥: maior ou igual
≤: menor ou igual
≠: diferente
Para solução dos problemas na maioria das vezes utilizamos a fórmula de Bhaskara igual na equação de 2º grau que só é diferente no sinal de igualdade (=) que é substituído pelos demais.
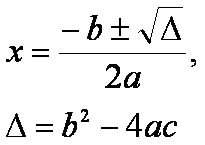
Exemplo:
Resolva a inequação (x + 4)(x – 4) < 0
No primeiro membro da inequação, há um produto notável conhecido como “produto da soma pela diferença”. Aplicando-o, podemos reescrever a inequação da seguinte forma:
(x + 4)(x – 4) < 0
x² – 16 < 0
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
x² < 16
– √16 < x < √16
– 4 < x < 4
Sendo assim, os valores de x para que a inequação seja válida são todos os números reais tais que – 4 < x < 4.
Exemplo 2:
Resolva a inequação do 2° grau (3x – 1)(x + 1) ≥ 0.
Primeiramente, vamos aplicar a propriedade distributiva para resolver a inequação:
(3x – 1)(x + 1) ≥ 0
3x² + 3x – x – 1 ≥ 0
3x² + 2x – 1 ≥ 0
Em seguida, usaremos a Fórmula de Bhaskara:
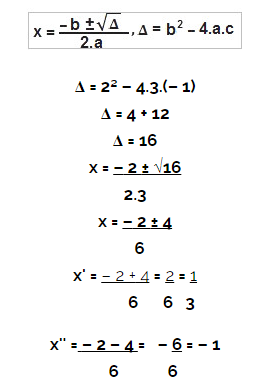
Portanto, os valores de x para que a inequação seja maior ou igual a zero são todos os números reais tais que ⅓ ≤ x ≤ – 1.
Fonte: Brasil escola, mundo educação e alunos online
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!