Funções do 1º e 2º graus – Problemas

COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!

 

Problemas envolvendo função de 1º grau

As funções são utilizadas na representação cotidiana de situações que envolvam valores constantes e variáveis, sempre colocando um valor em função do outro. Por exemplo, ao abastecermos o carro no posto de gasolina, o preço a ser pago depende da quantidade de litros de combustível colocada no tanque. Abordaremos as situações problemas ligadas às equações do 1º grau, respeitando a lei de formação f(x) = ax + b, com a ≠ 0.

Exemplo 1
Um motorista de táxi cobra R$ 3,50 de bandeirada (valor fixo) mais R$ 0,70 por quilômetro rodado (valor variável). Determine o valor a ser pago por uma corrida relativa a um percurso de 18 quilômetros.

Função que define o valor a ser cobrado por uma corrida de x quilômetros: f(x) = 0,70x + 3,50.

Valor a ser pago por uma corrida de percurso igual a 18 quilômetros.
f(x) = 0,70x + 3,50
f(18) = 0,70 * 18 + 3,50
f(18) = 12,60 + 3,50
f(18) = 16,10

O preço a ser pago por uma corrida com percurso igual a 18 quilômetros corresponde a R$ 16,10.

Exemplo 2

O preço de venda de um livro é de R$ 25,00 a unidade. Sabendo que o custo de cada livro corresponde a um valor fixo de R$ 4,00 mais R$ 6,00 por unidade, construa uma função capaz de determinar o lucro líquido (valor descontado das despesas) na venda de x livros, e o lucro obtido na venda de 500 livros.

Venda = função receita
R(x) = 25 * x

Fabricação: função custo
C(x) = 6 * x + 4

Lucro = receita – custo
L(x) = 25x – (6x + 4)
L(x) = 25x – 6x – 4
L(x) = 19x – 4

Lucro líquido será determinado pela função: L(x) = 19x – 4.

Lucro na venda de 500 livros

L(500) = 19 * 500 – 4
L(500) = 9 496

O lucro obtido na venda de 500 livros é de R$ 9 496,00.

Exemplo 3

O salário de um vendedor é composto de uma parte fixa no valor de R$ 800,00, mais uma parte variável de 12% sobre o valor de suas vendas no mês. Caso ele consiga vender R$ 450 000,00, calcule o valor de seu salário.

f(x) = 12% de x (valor das vendas mensais) + 800 (valor fixo)
f(x) = 12/100 * x + 800
f(x) = 0,12x + 800

f(450 000) = 0,12 * 450 000 + 800
f(450 000) = 54 000 + 800
f(450 000) = 54 800

O salário do vendedor será de R$ 54 800,00.

Fonte: Mundo Educação

 

Problemas envolvendo função de 2º grau

COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!

As funções do 2º grau possuem diversas aplicações na Matemática e auxiliam a Física em diversas situações nos movimentos de corpos na área da Cinemática e Dinâmica. A sua lei de formação, onde f(x) = ax² + bx + c, descreve uma trajetória parabólica de concavidade voltada para cima (decrescente – ponto mínimo) ou concavidade voltada para baixo (crescente – ponto máximo). Observe a resolução de situações problemas a seguir:

Exemplo 1

O movimento de um projétil, lançado para cima verticalmente, é descrito pela equação y = – 40x² + 200x. Onde y é a altura, em metros, atingida pelo projétil x segundos após o lançamento. A altura máxima atingida e o tempo que esse projétil permanece no ar correspondem, respectivamente, a:

Resolução:

Veja o gráfico do movimento:

 

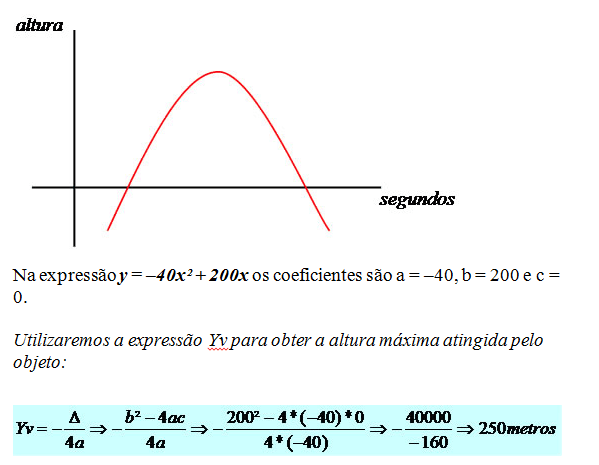
O objeto atingiu a altura máxima de 250 metros.

Utilizaremos a expressão Xv para obter o tempo de subida do objeto:

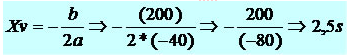
O projétil levou 2,5s para atingir altura máxima, levando mais 2,5s para retornar ao solo, pois no movimento vertical o tempo de subida é igual ao tempo de descida. Portanto, o projétil permaneceu por 5 s no ar.

Exemplo 2

Um objeto foi lançado do topo de um edifício de 84 m de altura, com velocidade inicial de 32 m/s. Quanto tempo ele levou para chegar ao chão? Utilize a expressão matemática do 2º grau d = 5t² + 32t, que representa o movimento de queda livre do corpo.

Resolução:

O corpo percorreu a distância de 84 m que corresponde à altura do edifício. Portanto, ao substituirmos d = 84, basta resolvermos a equação do 2º grau formada, determinando o valor do tempo t, que será a raiz da equação.

 

 

 

 

 

 

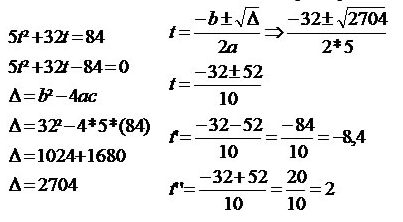
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!