COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
Funções polinomiais do 1º e 2º graus
Função polinomial do 1° grau
f(x) = ax + b
Onde a ≠ 0
a = coeficiente angular e
b = coeficiente linear
f(x) = imagem
x = domínio
Ex.: f(x) = 3x-1 onde a = 3 e b = -1
Nesta função o gráfico é uma reta
Função identidade
f(x) = x onde a = 1 e b = 0
Características principais: a é sempre igual a 1 e b é sempre igual a 0
Função linear
f(x) = 3x onde a = 3 e b = 0
Características principais: a ≠ 1 e 0 e b = 0
Função Afim
Esta é a função é a que representa melhor a função polinomial do 1° grau, onde tem autores que dizem que a função do 1° grau é a função afim.
f(x) = ax + b
Ex.: f(x) = 4x+2 onde a = 4 e b = 2
Características principais: a ≠ 0 e 1 e b ≠ 0
Raiz ou zero da função é todo valor de x que faz que f(x) seja nulo, ou seja, fique igual a zero.
Ex.: f(x) = 5x – 10
5x -10 = 0
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!
5x = 10
x = 10/5
x = 2
Substituindo na função você constatará que f(x) = 0
Vamos construir então um gráfico da seguinte função: y = x+3
Considerando x = 0
y = x + 3
y = 0 + 3
y = 3
Temos então um ponto (0,3)
Considerando y = 0
y = x + 3
0 = x + 3
x = -3
Temos outro ponto (-3, 0)
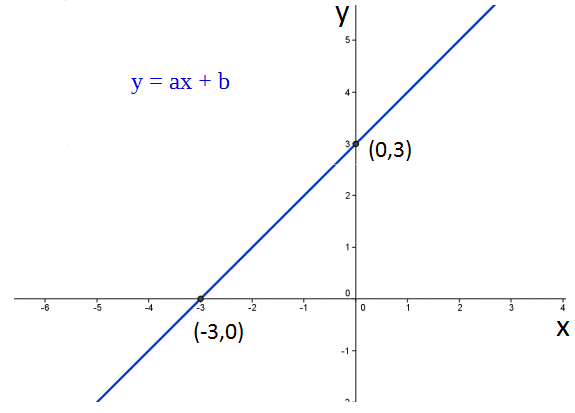
Função polinomial do 2° grau ou Função quadrática
Características:
Maior expoente da variável x é 2
f(x) = ax2 + bx + c onde a, b e c sejam reais e a ≠ 0
Sendo x o domínio e f(x) a imagem e a, b e c seus coeficientes
O gráfico é sempre uma parábola e se “a” for positivo a concavidade é para cima e se “a” for negativo a concavidade é para baixo.
Por ser uma parábola e não uma reta (1º Grau), o gráfico de uma função polinomial do 2° grau tem que ter mais de dois pares ordenado conhecidos. Acima de 7 pares já são suficientes para termos uma ideia da curva.
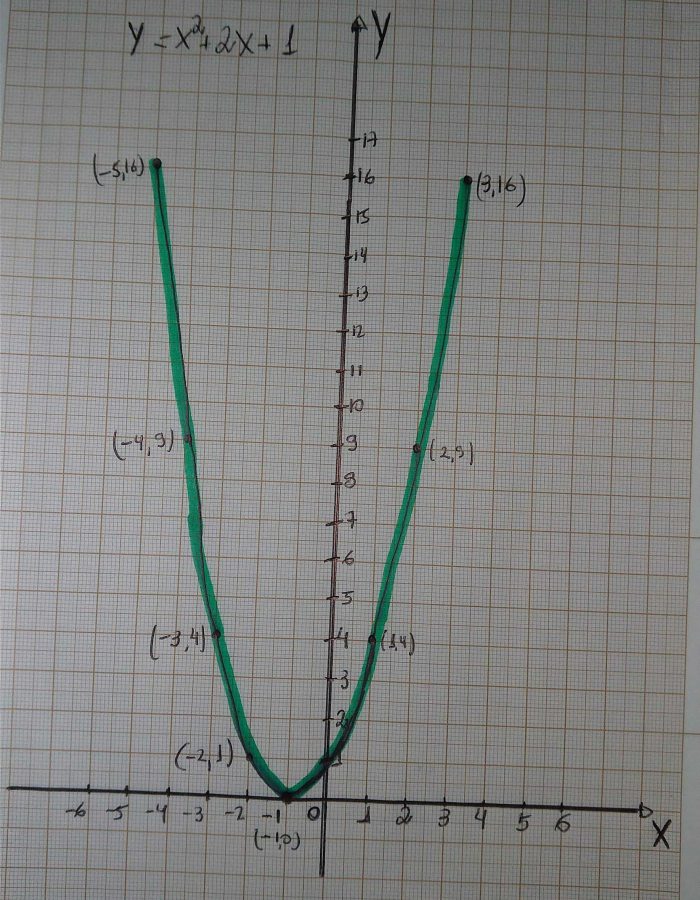
Vamos montar um gráfico da seguinte função:
y = x2 + 2x + 1
COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
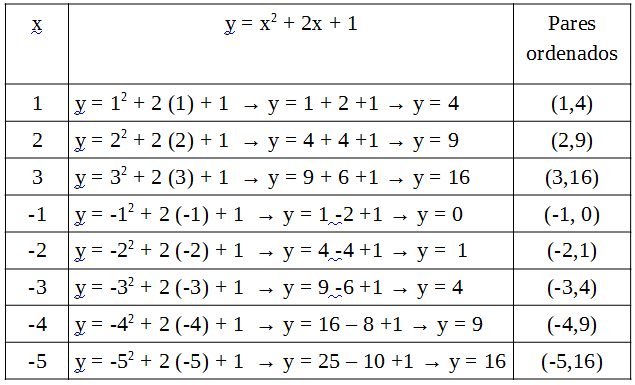
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!