COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
![]() Equação do 2º grau
Equação do 2º grau
Uma equação do 2º (segundo grau) é uma equação com duas incógnitas x, sendo que uma delas possuem um grau igual a 2.
Caso preferir, no vídeo abaixo tem esta postagem em áudio e vídeo
Ela é representada sob a forma ax² + bx +c = 0, em que a, b e c são constantes reais, onde a é diferente de zero (a ≠ 0).
Os parâmetros da equação são:
a – coeficiente principal
b – coeficiente secundário
c – termo independente
A equação do 2º grau pode ser completa ou incompleta:
Quando b ≠ 0 e c ≠ 0, a equação do 2º grau será considerada completa.
Ex.: x2 – 6x + 21 = 0= 0 é uma equação completa (a = 1, b = –6 e c = 21).
Quando b = 0 ou c = 0 ou b = c = 0, a equação do 2º grau será considerada incompleta.
Exs.:
ax2 + c = 0 é uma equação incompleta (b=0). Ex.: 2x² + 20 = 0
ax2 + bx = 0 é uma equação incompleta (c = 0). Ex.: 5x² +6x = 0
ax2 = 0 é uma equação incompleta (b = c = 0). Ex.: 4x² = 0
(neste caso a raiz x sempre será zero x1=x2 = 0)
Fórmula de Bhaskara
Toda equação do segundo grau pode apresentar até duas soluções diferentes. Em todos os casos estas soluções podem ser obtidas pela fórmula de Bhaskara.
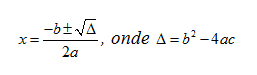
Δ = Delta
As soluções da equação do segundo grau são chamadas de raízes da equação (x1 e x2).
Se Δ > 0, então a equação admite duas raízes (duas soluções em R);
Se Δ = 0, então a equação admite duas raízes iguais (uma única solução em R);
Se Δ < 0, ou seja, Δ for negativo, a equação não admite solução em R.
Nós temos 3 maneiras de resolver uma equação do 2º grau:
1 – Resolução de Equação de 2º Grau completa
Na resolução de uma equação de 2º Grau completa nós utilizamos a Fórmula de Bhaskara.
Vamos resolver uma questão de concurso para ficar mais fácil a compreensão:
Ano: 2023 Banca: CETREDE Órgão: Prefeitura de Guaiúba – CE Cargo: Professor
Calcule e encontre as raízes da equação: 3x2 + 4x – 15 = 0. Marque a opção CORRETA.
A x1 = 3; x2 = 5.
B x1 = – 3; x2 = 3.
C x1 = – 3; x2 = 5/3.
D x1 = 3; x2 = 5/3.
E x1 = – 5; x2 = 3/5.
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
Resolução:
3x2 + 4x – 15 = 0
ax² + bx +c = 0
a = 3
b = 4
c = -15
Primeiro achamos o valor de delta:
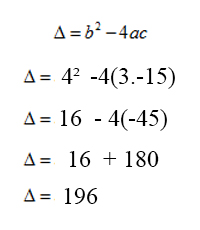
Agora utilizamos a Fórmula de Bhaskara:
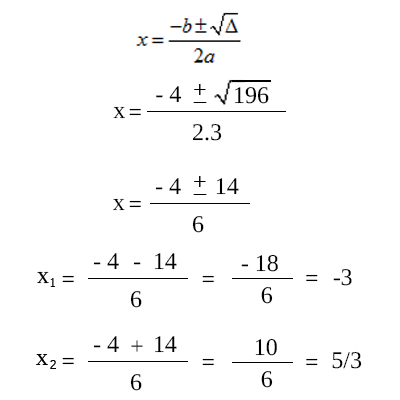
RESPOSTA DA QUESTÃO LETRA C
2 – Resolução de Equação de 2º Grau incompleta ax2 + bx = 0 onde c=0
Ela também pode ser resolvida com a Fórmula de Bhaskara, mas existe um método mais rápido de resolver.
Para Encontrarmos a solução é só colocar a variável x em evidência.
Vamos resolver uma equação que já caiu em concurso:
2x² + 6x = 0
Agora vamos colocar a variável x em evidência:
2x² + 6x = 0
x(2x + 6) = 0
Então fica agora:
x = 0 e 2x+6 = 0
2x+6 = 0
2x = -6
x = -6/2
x = -3
Então a solução é:
S = {0,-3}
3 – Resolução de Equação de 2º Grau incompleta ax2 + c = 0 onde b=0
Neste caso vamos isolar a variável x:
Vamos então resolver uma questão para melhor entendimento:
2x2 – 8 = O
Isolamos a variável x:
2x2 = 8
x2 = 8/2
x2 = 4
x = √4
Ao extrair a raiz, temos que lembrar que a equação do 2 Grau tem duas raízes em sua solução, ou seja, colocamos o símbolo de ±.”
x = ± 2
S= {2, -2}
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!


