COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
POTENCIAÇÃO
A potenciação é uma multiplicação de fatores iguais
Exemplos:
1) (1,5)² = 1,5 x 1,5 = 2,25
2) (0,4)³ = 0,4 x 0,4 x 0,4 = 0,064
vamos lembrar que: são válidas as convenções para os expoentes um e zero.
Exemplos
1) (7,53)¹ = 7,53
2) ( 2,85)⁰ = 1
A operação realizada na potenciação é uma multiplicação e é representada da seguinte forma:
an = a . a . a . a …
a = base
n = expoente
a . a . a . a … = produto de n fatores iguais que gera como resultado a potência
Para compreender melhor, acompanhe os exemplos abaixo:
⇒ 23 = 2 . 2 . 2 = 8
2 = base
3 = expoente
2 . 2 . 2 = produto de fatores
8 = potência
Como o expoente é 3, tivemos que repetir a base, que é 2 três vezes, em um produto.
⇒ 54 = 5 . 5 . 5 . 5 = 625
5 = base
4 = expoente
5 . 5 . 5 . 5 = produto de fatores
625 = potência
Como o expoente é 4, tivemos que repetir a base, que é 5 quatro vezes, em um produto.
⇒ 102 = 10 . 10 = 100
10 = base
2 = expoente
10 . 10 = produto de fatores
100 = potência
Como o expoente é 2, tivemos que repetir a base, que é 10 duas vezes, em um produto.
Tipos de potenciação
- Base real e expoente inteiroQuando o expoente é inteiro, significa que ele pode possuir número negativo ou positivo.
⇒ Expoente positivo: Quando a base for um número real e o expoente for positivo, obteremos a potência efetuando o produto dos fatores. Acompanhe alguns exemplos:
2+2 = 2 . 2 = 4
0,3+3 = 0,3 . 0,3 . 0,3 = 0,027
(½ )+2 = ½ . ½ = ¼
⇒ Expoente negativo: Se o expoente é negativo, devemos fazer o inverso do número, que é trocar numerador com denominador, para o expoente passar a ser positivo. Observe alguns exemplos:
2-2 = (1/2)² = 1/4
0,3 – 3 = (3/10)–³ = (10/3)³ = 1000/ 27 = 37,037
(½ )-2 = (2/1)+2 = 2 . 2 = 4
⇒ Expoente igual a 1
Quando o expoente for igual a um positivo, a potência será o próprio número da base. Veja os exemplos abaixo:
a1 = a
21 = 2
41 = 4
1001 = 100
⇒ Expoente igual a 0
Se o expoente for 0, a reposta referente à potência sempre será 1. Acompanhe os exemplos:
a0 = 1
10000 = 1
250 = 1
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
Propriedades da potenciação
As propriedades da potenciação são utilizadas para simplificar os cálculos. Há, no total, cinco propriedades:
- Produto de potências de mesma base: conserva a base e soma os expoentes. Exemplos:an . am = an + m
22 . 23 = 22 + 3 = 25
45 . 42 = 45 + 2 = 47 - Divisão de potências de mesma base: conserva a base e subtrai os expoentes. Exemplos:an : am = an = an – m
am
56 : 52 = 56 = 56 – 2 = 54
52
92 : 93 = 92 = 92 – 3 = 9-1
93 - Potência de potência: devemos multiplicar os expoentes. Exemplos:(an)m = an . m
(74)2 = 74 . 2 = 78
(123)2 = 123 . 2 = 126 - Potência de um produto: o expoente geral é expoente dos fatores. Exemplos:(a . b)n = ( an . bn)
(4 . 5)2 = (42 . 52)
(12 . 9)3 = (123 . 93) - Multiplicação de potências com o mesmo expoente: conserva o expoente e multiplica as bases. Exemplo:an . bn= (a . b)n
42 . 62 = (4 . 6)2
73 . 43 = (7 . 4)3
1) Calcule as potências
a) ( 0,7)²= 0,49
b) (0,3) ²= 0,09
c) (1,2) ²= 1,44
d) (2,5) ²= 6,25
e) (1,7) ²= 2,89
f) (8,4) ²= 70,56
g) (1,1)³= 1,331
h) (0,1)³= 0,001
i) (0,15) ²= 0,0225
j) (0,2)⁴= 0,0016
2) Calcule o valor das expressões
a) (1,2)³ + 1,3 = 3,028
b) 20 – (3,6) ² = 7,04
c) (0,2) ² + (0,8) ² = 0,68
d) (1,5) ² – (0,3) ² = 2,16
e) 1 – (0,9) ² = 0,19
f) 100 x (0,1)⁴ = 0,01
g) 4² : 0,5 – (1,5) ² = 29,75
h) ( 1 – 0,7) ² + ( 7 – 6)⁵= 1,09
Radiciação
A radiciação é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões aritméticas e algébricas. Vamos definir essa operação e analisar suas propriedades.
Dados um número real não negativo x e um número natural n ≥ 1, chama-se raiz enésima de x o número real não negativo y tal que yn = x. O símbolo utilizado para representar a raiz enésima de x é ![]() e é chamado de radical. Nesse símbolo, x é o radicando e n é o índice.
e é chamado de radical. Nesse símbolo, x é o radicando e n é o índice.
Pela definição de radiciação, temos que:
![]()
Raiz com índice par
Para um número real a positivo, com n sendo um número natural par e positivo, maior que 1, tem-se um b, tal que, se a−−√n=b, então bn = a, onde a é o radicando, n é o índice, b é raiz e √ é o radical. Com ![]() .
.
Nenhum valor de a negativo (-a) tem definição nesse caso.
Observação: quando o índice não aparecer no radical, isso indica que n = 2 e teremos uma raiz quadrada.
Exemplos:

Raiz com índice ímpar
Sendo a um número real, positivo ou negativo, com m sendo um número natural ímpar e positivo, maior que 1, tem-se um b, tal que, se a−−√m=b, então bm = a, onde a é o radicando, m é o índice, b é raiz e √ é o radical. Com ![]() .
.
Nesse caso é possível obtermos raízes negativas dentro do conjunto dos números reais (ℝ).
Exemplos:
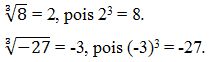
Propriedades
- Para o radicando que tenha, como resultado de uma fatoração, expoente igual a seu índice, então este radicando é igual à raiz procurada.
 Exemplos:
Exemplos:
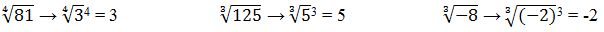
- Podemos dividir o radicando e o índice por um mesmo número real, desde que este seja diferente de zero e maior que um, e divisor comum do radicando e do índice.
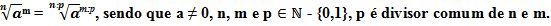
Exemplos:
- Para resolvermos a raiz m-esima de uma raiz n-ésima, multiplicamos os índices entre si mantendo intacto o radical interno.
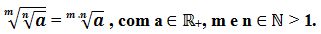 Exemplos:
Exemplos:

- A raiz n-ésima de um produto é igual ao produto das raízes n-ésimas.
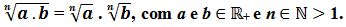 Exemplos:
Exemplos:

- A raiz n-ésima de um quociente (divisão) de a por b é igual ao quociente entre as raízes n-ésimas.
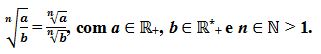 Exemplos:
Exemplos:
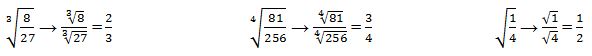
Fontes: Mundo educação e Info escola
TRANSFORMAÇÃO DE FRAÇÕES EM NÚMEROS DECIMAIS
Para transformar uma fração em números decimais, basta dividir o numerador pelo denominador (obs o numerador é o números de cima da fração e o denominador o números debaixo)
Exemplos
transformar em números decimais as frações irredutíveis
1) 5/4 = 5 : 4 = 1,25 que será um, número decimal exato
2) 7/9 = 7 : 9 = 0,777… é uma dizima periódica simples
3) 5/6 = 5: 6 = 0,8333…… é uma dizima periódica composta
outros exemplos
a) 4,666… dízima periódica simples (período 6)
b) 2,1818….dízima periódica simples ( período 18)
c) 0,3535…. dízima periódica simples (período 35)
d) 0,8777…. dízima periódica composta (período 7 e parte não periódica 8 )
e) 5,413333…. dízima periódica composta (período 3 e parte não periódica 41)
EXERCÍCIOS
1) Transforme em números decimais as frações:
a) 10/4 =
b) 4/5 =
c) 1/3 =
d) 5/3 =
e) 14/5 =
f) 1/6 =
g) 2/11 =
h) 43/99 =
i) 8/3 =
2) Transforme as frações decimais em números decimais :
a) 9/10 = (R: 0,9)
b) 57/10 = (R: 5,7)
c) 815/10 = (R: 8,15)
d) 3/100 = (R: 0,03)
e) 74/100 = (R: 0,74)
f) 2357/1000 = (R: 2,357)
g) 7/1000 = (R: 0,007)
h) 15/10000 = (R: 0,0015)
i) 4782/10000 = (R: 0,4782)
Esta matéria foi retirada do Blog JMP25
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!



Essa explicação de expoente negativo ficou um pouco confusa por ter a conversão da base misturada:
2-2 = 1 = 1 . 1 = 1
2+2 2 2 4
Pelo que eu entendi, 2 elevado a menos dois, seria (1 sobre 2), certo? De onde saiu este resultado de \”1\”?
Oi Francis realmente estava confuso e errado. Refiz ela de uma maneira que acredito que fica mais fácil a compreensão
Abraços
Agora sim ficou ótimo! 🙂
Para **potenciação**, você se esqueceu das respostas.
Aqui vão elas, peço que as confira antes, por gentileza:
(1)
a) 0,49
b) 0,09
c) 1,44
d) 6,25
e) 2,89
f) 70,56
g) 1,331
h) 0,001
i) 0,0225
j) 0,0016
(2) –> Aqui foram feitos os cálculos e logo à direita de cada, temos a resposta:
a) (1,2 . 1,2 . 1,2) + 1,3 = 3,028
b) 20 – (3,6 . 3,6) = 20 – 12,96 = 7,04
c) (0,2 . 0,2) – (0,8 . 0,8) = 0,04 – 0,64 = 0,6
d) (1,5 . 1,5) – (0,3 . 0,3) = 2,25 – 0,09 = 2,16
e) 1 – (0,9 . 0,9) = 1 – 0,81 = 0,19
f) 100 x (0,1 . 0,1 . 0,1 . 0,1) = 100 x 0,0001 = 0,01
g) 16 : 0,5 – (1,5 . 1,5) = 32 – 2,25 = 29,75
h) (1² – 0,7²) + (7² – 6²) = (1 – 0,49) + (49 – 36) = 0,51 + 13 = 13,51
Thanks! 😀
Oi Francis muito obrigado pela disposição de verificar todas as questões. Teve duas que estão incorretas o resultado: 2c= 0,68 na questão é uma soma e não subtração. 2h= 1,09. Neste você deve observar duas coisas. 7-6 é elevado a 5 e não dois. Outra coisa bem importante é que a regra de potenciação quando dentro dos parenteses é uma soma ou subtração você deve primeiro somar ou diminuir para depois elevar a potência. Você usou a mesma regra de multiplicação e divisão, na qual tanto faz você multiplicar ou dividir primeiro ou elevar primeiro, o resultado sempre será o mesmo. Já na soma e subtração não. Levando este exercício como exemplo você viu que 1-0,7 elevado a 2 no seu deu 0,51 no qual deveria dar 0,09.
Abraços e novamente obrigado.
Obrigado!! A 2c foi falta de atenção e as demais eu não li direito a regra da potência entre parênteses com adição ou subtração.