COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
No final da postagem tem duas videoaulas. E você, qual o concurso você vai fazer? Deixe um comentário para mim, pois posso fazer postagens direcionadas para ele e te ajudar mais. Aproveita também para inscrever seu e-mail para receber conteúdos todos os dias.
Dica: Para você que não esta encontrando o conteúdo que precisa ou prefere estudar por apostilas dá uma olhada no site Apostilas Opção, lá eles tem praticamente todas as apostilas atualizadas de todos os concursos abertos.
Bons estudos!
Sistema de equação do 2º Grau
 Os sistemas de equações nada mais são do que estratégias que nos permitem resolver problemas e situações que envolvem mais de uma variável e pelo menos duas equações. Se as equações presentes no sistema envolverem apenas a adição e a subtração das incógnitas, dizemos que se trata de um sistema de equações do 1° grau. Podemos resolver esse sistema de duas formas, através da representação gráfica ou algebricamente. Na forma algébrica, dispomos de duas alternativas, o método da adição ou da substituição.
Os sistemas de equações nada mais são do que estratégias que nos permitem resolver problemas e situações que envolvem mais de uma variável e pelo menos duas equações. Se as equações presentes no sistema envolverem apenas a adição e a subtração das incógnitas, dizemos que se trata de um sistema de equações do 1° grau. Podemos resolver esse sistema de duas formas, através da representação gráfica ou algebricamente. Na forma algébrica, dispomos de duas alternativas, o método da adição ou da substituição.
No caso de uma multiplicação entre as incógnitas ou, simplesmente, de uma delas aparecer como uma potência de expoente 2, dizemos que o sistema envolve também equações de 2° grau. Para resolver um sistema desse tipo, as estratégias são as mesmas citadas anteriormente, mas podem haver mais soluções nesse caso.
Exemplo 1
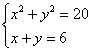
Isolando x ou y na 2ª equação do sistema:
x + y = 6
x = 6 – y
Substituindo o valor de x na 1ª equação:
x² + y² = 20
(6 – y)² + y² = 20
(6)² – 2 * 6 * y + (y)² + y² = 20
36 – 12y + y² + y² – 20 = 0
16 – 12y + 2y² = 0
2y² – 12y + 16 = 0 (dividir todos os membros da equação por 2)
y² – 6y + 8 = 0
∆ = b² – 4ac
∆ = (–6)² – 4 * 1 * 8
∆ = 36 – 32
∆ = 4
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
a = 1, b = –6 e c = 8
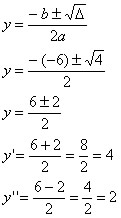
Determinando os valores de x em relação aos valores de y obtidos:
Para y = 4, temos:
x = 6 – y
x = 6 – 4
x = 2
Par ordenado (2; 4)
Para y = 2, temos:
x = 6 – y
x = 6 – 2
x = 4
Par ordenado (4; 2)
S = {(2: 4) e (4; 2)}
Fonte: mundo educação e Brasil escola
https://www.youtube.com/watch?v=7-NdRWRC4jM
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!


