Números racionais: operações e propriedades

Números racionais: operações e propriedades

Números Racionais

Interseção dos conjuntos: Naturais, Inteiros e Racionais.

Os números decimais são aqueles números que podem ser escritos na forma de fração.

Podemos escrevê-los de algumas formas diferentes:
Por exemplo:

♦ Em forma de fração ordinária:  ; ; e todos os seus opostos.

Esses números tem a forma  com a ,  b  Z  e  b ≠ 0.

♦ Números decimais com finitas ordens decimais ou extensão finita:

Esses números têm a forma  com a , b  Z e b ≠ 0.

♦ Número decimal com infinitas ordens decimais ou de extensão infinita periódica. São dízimas periódicas simples ou compostas:

As dízimas periódicas de expansão infinita, que podem ser escritas na forma  : com a, b  Z e b ≠ 0.

► O conjunto dos números racionais é representado pela letra Q maiúscula.

Q = {x = , com a Z e b Z*}

►Outros subconjuntos de Q:

Além de N e Z, existem outros subconjuntos de Q.

Q^* ———- É o conjunto dos números racionais diferentes de zero.

Q₊ ———- É o conjunto dos números racionais positivos e o zero.

Q_– ———– É o conjunto dos números racionais negativos e o zero.

Q_^*+ ———- É o conjunto dos números racionais positivos.

Q^*_– ———– É o conjunto dos números racionais negativos.

► Representação Geométrica

Entre dois números racionais existem infinitos outros números racionais.

Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola

 

Operações com números racionais

 Adição e Subtração

 

Para simplificar a escrita, transformamos a adição e subtração em somas algébricas. Eliminamos os parenteses e escrevemos os números um ao lado do outro, da mesma forma como fazemos com os números inteiros.

Exemplo 1: Qual é a soma:

 

 

Exemplo 2: Calcule o valor da expressão

 

 

   

 

 

 

 

Multiplicação e divisão

Na multiplicação de números racionais, devemos multiplicar numerador por numerador, e denominador por denominador, assim como é mostrado nos exemplos abaixo:

 

 

 

 

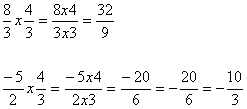
Na divisão de números racionais, devemos multiplicar a primeira fração pelo inverso da segunda, como é mostrado no exemplo abaixo:

 

 

   

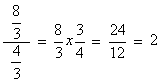
Potenciação e radiciação

Na potenciação, quando elevamos um número racional a um determinado expoente, estamos elevando o numerador e o denominador a esse expoente, conforme  os exemplos abaixo:

 

 

 

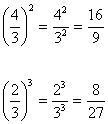
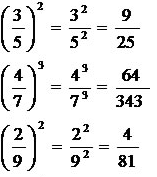
Expoente Negativo 

Nos casos em que o expoente é negativo, devemos trocar o sinal do expoente e inverter a base racional, isto é, o numerador passa a ser denominador e o denominador passa a ser numerador. Observe:

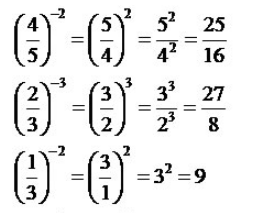
Na radiciação, quando aplicamos a raiz quadrada a um número racional, estamos aplicando essa raiz ao numerador e ao denominador, conforme o exemplo abaixo:

 

 

 

Fonte: Só Matemática

Exercícios sobre frações e números racionais
1. Qual alternativa representa a fração 9/2 em números decimais?
(a) 3,333    (b) 4,25    (c) 5,01    (d) 4,5
Resp: d

2. Qual alternativa representa a fração 35/1000 em números decimais?
(a) 0,35    (b) 3,5    (c) 0,035    (d) 35
Resp: c

3. Assinalar a alternativa com a resposta da adição 4/7+2/7:
(a) 5/7    (b) 6/14      (c) 7/6      (d) 6/7
Resp: d

4. Qual das alternativas representa a subtração 8/9-6/9?
(a) −2/9      (b) 2/9      (c) 14/9      (d) 1/4

Resp: b