![]() Operações com conjuntos
Operações com conjuntos
União de conjuntos: AUB é formado por todos os elementos que pertence ao conjunto A e conjunto B
![]() Operações com conjuntos
Operações com conjuntos
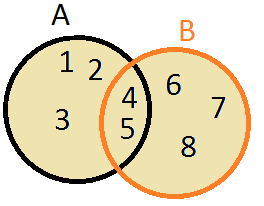
União de conjuntos: AUB é formado por todos os elementos que pertence ao conjunto A e conjunto B

Linguagem dos conjuntos
As noções de conjunto e elemento, em matemática, são noções primitivas, isto é, não são definidas. A ideia de conjunto é a mesma de coleção.
Os conjuntos são representados por letras maiúsculas e os elementos do mesmo são representados entre chaves. Assim, teríamos:
O conjunto das letras do nosso alfabeto; L= {a, b, c, d,…, z}.
O conjunto dos dias da semana: S= {segunda, terça,… domingo}.
No final da postagem tem uma videoaula para complementar o assunto.
Recomendo os seguintes links:
Como estudar para concursos públicos.
Conheça as características das principais bancas organizadoras de concursos públicos
Gostaria de lembrar também que tenho um livro de aventura que publiquei a versão final em e-book no Amazon, A fortaleza do Centro, dá uma olhadinha nele é muito legal.
Gostaria também de saber qual concurso você vai fazer, é só postar nos comentários
Abraços e bons estudos!
Os Números Irracionais (I) fazem parte do conjunto dos Números Reais (R) junto com os Números Racionais (Q),
Números Reais
O conjunto dos números reais surge para designar a união do conjunto dos números racionais e o conjunto dos números irracionais. É importante lembrar que o conjunto dos números racionais é formado pelos seguintes conjuntos: Números Naturais e Números Inteiros. Vamos exemplificar os conjuntos que unidos formam os números reais. Veja:
Números Naturais (N): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ….
Números Inteiros (Z): …, –8, –7, –6, –5, –4, –3, – 2, –1, 0, 1, 2, 3, 4, 5, 6, 7, 8, …..
Números Racionais (Q): 1/2, 3/4, 0,25, –5/4,
Números Irracionais (I): √2, √3, –√5, 1,32365498…., 3,141592….
Podemos concluir que o conjunto dos números reais é a união dos seguintes conjuntos:
N U Z U Q U I = R ou Q U I = R
Os números reais podem ser representados por qualquer número pertencente aos conjuntos da união acima. Essas designações de conjuntos numéricos existem no intuito de criar condições de resolução de equações e funções, as soluções devem ser dadas obedecendo aos padrões matemáticos e de acordo com a condição de existência da incógnita na expressão.
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
Coloquei mais um pouco da matéria para você que quer aprofundar mais no assunto:
O conjunto dos números reais é formado pela união entre o conjunto dos números racionais e o conjunto dos números irracionais. Existem várias propriedades a respeito dos números reais, que são extensões das propriedades dos números racionais. Essas propriedades estão relacionadas com a ordem dos números reais e com o estudo das operações matemáticas básicas aplicadas aos elementos desse conjunto.
A definição dos números reais depende das definições dos conjuntos dos números racionais e irracionais, que, por sua vez, dependem da definição dos números inteiros. Dessa maneira, todos os números geralmente estudados até o final do Ensino Fundamental e início do Ensino Médio são os números reais.
De posse da definição de números reais, discutiremos as propriedades mais importantes relacionadas com esse conjunto numérico.
Propriedades do conjunto dos números reais
As propriedades a seguir são decorrentes da definição dos números reais e também da inclusão das operações “adição” e “multiplicação” entre os elementos desse conjunto.
→ O conjunto dos números reais é um conjunto completo
Existe uma relação feita entre o conjunto dos números reais e a reta numérica, que é construída da seguinte maneira: para cada número real, existe um e apenas um ponto representando-o na reta numérica. É possível mostrar que a reta não contém nenhum “furo”, isto é, ponto que não represente número real algum. Portanto, o conjunto dos números reais é completo.
→ O conjunto dos números reais é um conjunto ordenado
Ainda avaliando a reta numérica, comparando dois números reais quaisquer, aquele que estiver mais à esquerda é menor do que aquele que estiver mais à direita. Além disso, se estiverem no mesmo ponto, serão iguais. Essa é a ordenação do conjunto dos números reais representada na reta numérica.
Propriedades operatórias dos números reais
Dados os números reais “a”, “b” e “c”, as seguintes propriedades operatórias são válidas:
1 – Associatividade:
a·(b·c) = (a·b)·c
a + (b + c) = (a + b) + c
2 – Comutatividade:
a·b = b·a
a + b = b + a
3 – Existência de elemento neutro único para a soma e para a multiplicação:
a + 0 = a
a·1 = a
4 – Existência de elemento inverso único para a soma e para a multiplicação:
a + (– a) = 0
a· 1 = 1
a
5 – Distributividade:
a · (b + c) = a·b + a·c
Por Luiz Paulo Moreira
Graduado em Matemática
Números racionais: operações e propriedades
Números Racionais

Interseção dos conjuntos: Naturais, Inteiros e Racionais.
Os números decimais são aqueles números que podem ser escritos na forma de fração.
Podemos escrevê-los de algumas formas diferentes:
Por exemplo:
Números inteiros
Introdução aos números inteiros
Na época do Renascimento, os matemáticos sentiram cada vez mais a necessidade de um novo tipo de número, que pudesse ser a solução de equações tão simples como:
x + 2 = 0, 2x + 10 = 0, 4y + 4 = 0
As Ciências precisavam de símbolos para representar temperaturas acima e abaixo de 0º C, por exemplo. Os astrônomos e físicos estavam procurando uma linguagem matemática capaz de expressar o movimento de atração entre dois corpos. Quando um corpo age com uma força sobre outro corpo, este reage com uma força de mesma intensidade e sentido contrário.
Mas a tarefa não ficava somente em criar um novo número, era preciso encontrar um símbolo que permitisse operar com esse número criado, de modo prático e eficiente.
Sobre a origem dos sinais
A idéia sobre os sinais vem dos comerciantes da época. Os matemáticos encontraram a melhor notação para expressar esse novo tipo de número. Veja como faziam tais comerciantes:
Suponha que um deles tivesse em seu armazém duas sacas de feijão com 10 kg cada. Se esse comerciante vendesse num dia 8 Kg de feijão, ele escrevia o número 8 com um traço (semelhante ao atual sinal de menos) na frente para não se esquecer de que no saco faltava 8 Kg de feijão.
Mas se ele resolvesse despejar no outro saco os 2 Kg que restaram, escrevia o número 2 com dois traços cruzados (semelhante ao atual sinal de mais) na frente, para se lembrar de que no saco havia 2 Kg de feijão a mais que a quantidade inicial.
Com essa nova notação,os matemáticos poderiam, não somente indicar as quantidades, mas também representar o ganho ou a perda dessas quantidades, através de números, com sinal positivo ou negativo.
O conjunto Z dos Números Inteiros
Definimos o conjunto dos números inteiros como a reunião do conjunto dos números naturais{1, 2, 3…}, o conjunto dos opostos dos números naturais{ -1, -2, …} e o zero. Este conjunto é denotado pela letra Z (Zahlen=número em alemão). Este conjunto pode ser escrito por:
Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4,…}
Exemplos de subconjuntos do conjunto Z:
Conjunto dos números inteiros exceto o número zero:
Z* = {…, -4, -3, -2, -1, 1, 2, 3, 4,…}
Conjunto dos números inteiros não negativos:
Z+ = {0, 1, 2, 3, 4,…}
Conjunto dos números inteiros não positivos:
Z- = {…, -4, -3, -2, -1, 0}
Observação: Não existe padronização para estas notações.
Reta Numerada
Uma forma de representar geometricamente o conjunto Z é construir uma reta numerada, considerar o número 0 como a origem e o número 1 em algum lugar, tomar a unidade de medida como a distância entre 0 e 1 e por os números inteiros da seguinte maneira:
Ao observar a reta numerada notamos que a ordem que os números inteiros obedecem é crescente da esquerda para a direita, razão pela qual indicamos com uma seta para a direita. Esta consideração é adotada por convenção, o que nos permite pensar que se fosse adotada outra forma, não haveria qualquer problema.
Baseando-se ainda na reta numerada podemos afirmar que todos os números inteiros possuem um e somente um antecessor e também um e somente um sucessor.
Ordem no conjunto Z
O sucessor de um número inteiro é o número que está imediatamente à sua direita na reta (em Z) e o antecessor de um número inteiro é o número que está imediatamente à sua esquerda na reta (em Z).
Exemplos:
3 é sucessor de 2;
-5 é antecessor de -4
0 é antecessor de 1
-1 é sucessor de -2
Simetria no conjunto Z
Todo número inteiro z exceto o zero, possui um elemento denominado simétrico ou oposto -z e ele é caracterizado pelo fato geométrico que tanto z como -z estão à mesma distância da origem do conjunto Z que é 0.
Exemplos:
O oposto de ganhar é perder;
O oposto de perder é ganhar;
O oposto de 3 é -3
O oposto de 5 é -5
Módulo de um número Inteiro
O módulo ou valor absoluto de um número Inteiro é definido como sendo o maior valor entre um número e seu elemento oposto e pode ser denotado pelo uso de duas barras verticais | |. Assim:
|x| = max{-x,x}
Exemplos:
|0| = 0
|8| = 8
|-6| = 6
Observação: Do ponto de vista geométrico, o módulo de um número inteiro corresponde à distância deste número até a origem (zero) na reta numérica inteira.
A soma (adição) de números inteiros
Para melhor entendimento desta operação, associaremos aos números inteiros positivos a idéia de ganhar e aos números inteiros negativos a idéia de perder.
ganhar 3 + ganhar 4 = ganhar 7
(+3) + (+4) = (+7)
perder 3 + perder 4 = perder 7
(-3) + (-4) = (-7)
ganhar 8 + perder 5 = ganhar 3
(+8) + (-5) = (+3)
perder 8 + ganhar 5 = perder 3
(-8) + (+5) = (-3)
Atenção: O sinal (+) antes do número positivo pode ser dispensado, mas o sinal (-) antes do número negativo nunca pode ser dispensado.
Exemplos:
-3 + 3 = 0
6 + 3 = 9
5 – 1 = 4
Propriedades da adição de números inteiros
Fecho: O conjunto Z é fechado para a adição, isto é, a soma de dois números inteiros ainda é um número inteiro.
Associativa: Para todos a,b,c em Z:
a + ( b + c ) = ( a + b ) + c
2 + ( 3 + 7 ) = ( 2 + 3 ) + 7
Comutativa: Para todos a,b em Z:
a + b = b + a
3 + 7 = 7 + 3
Elemento neutro: Existe 0 em Z, que adicionado a todo z em Z, proporciona o próprio z, isto é:
z + 0 = z
7 + 0 = 7
Elemento oposto: Para todo z em Z, existe (-z) em Z, tal que
z + (-z) = 0
9 + (-9) = 0
A Multiplicação (produto) de números inteiros
A multiplicação funciona como uma forma simplificada de uma adição quando os números são repetidos. Poderiamos analisar tal situação como o fato de estarmos ganhando repetidamente alguma quantidade, como por exemplo, ganhar 1 objeto por 30 vezes consectivas, significa ganhar 30 objetos e esta repetição pode ser indicada por um x, isto é:
1 + 1 + 1 + … + 1 + 1 = 30 x 1 = 30
Se trocarmos o número 1 pelo número 2, teremos:
2 + 2 + 2 + … + 2 + 2 = 30 x 2 = 60
Se trocarmos o número 2 pelo número -2, teremos:
(-2) + (-2) + … + (-2) = 30 x (-2) = -60
Observamos então que a multiplicação é um caso particular da adição onde os valores são repetidos.
Na multiplicação o produto dos números a e b, pode ser indicado por axb, a.b ou ainda ab sem nenhum sinal entre as letras.
Para realizar a multiplicação de números inteiros, devemos obedecer à seguinte regra de sinais:
(+1) x (+1) = (+1)
(+1) x (-1) = (-1)
(-1) x (+1) = (-1)
(-1) x (-1) = (+1)
Podemos assim concluir que:
Sinais iguais produto de inteiros é positivo.
Sinais diferentes produto de inteiros é negativo.
Propriedades da multiplicação de números inteiros
Fecho: O conjunto Z é fechado para a multiplicação, isto é, a multiplicação de dois números inteiros ainda é um número inteiro.
Associativa: Para todos a,b,c em Z:
a x ( b x c ) = ( a x b ) x c
2 x ( 3 x 7 ) = ( 2 x 3 ) x 7
Comutativa: Para todos a,b em Z:
a x b = b x a
3 x 7 = 7 x 3
Elemento neutro: Existe 1 em Z, que multiplicado por todo z em Z, proporciona o próprio z, isto é:
z x 1 = z
7 x 1 = 7
Elemento inverso: Para todo z em Z, z diferente de zero, existe z-1=1/z em Z, tal que
z x z-1 = z x (1/z) = 1
9 x 9-1 = 9 x (1/9) = 1
Propriedade mista (distributiva)
Distributiva: Para todos a,b,c em Z:
a x ( b + c ) = ( a x b ) + ( a x c )
3 x ( 4 + 5 ) = ( 3 x 4 ) + ( 3 x 5 )
Potenciação de números inteiros
Definição: A potência an do número inteiro a, é definida como um produto de n fatores iguais. O número a é denominado a base e o número n é o expoente.
an = a x a x a x a x … x a
n vezes
Exemplos:
23 = 2 x 2 x 2 = 8
(-2)3 = (-2) x (-2) x (-2) = (-8)
(-5)2 = (-5) x (-5) = 25
(+5)2 = (+5) x (+5) = 25
com os exemplos acima, podemos observar que a potência de todo número inteiro elevado a um expoente par é um número positivo e a potência de todo número inteiro elevado a um expoente ímpar é um número que conserva o seu sinal.
Observação: Quando o expoente é n=2, a potência a2 pode ser lida como: “a elevado ao quadrado” e quando o expoente é n=3, a potência a3 pode ser lida como: “a elevado ao cubo”. Tais leituras são provenientes do fato que área do quadrado pode ser obtida por A=a2 onde a é o lado e o volume do cubo pode ser obtido por V=a3 onde a é o lado do cubo.
Radiciação de números inteiros
Definição: A raiz n-ésima (de ordem n) de um número inteiro a é a operação que resulta em um outro número inteiro não negativo b que elevado à potência n fornece o número a. O número n é o índice da raiz enquanto que o número a é o radicando (que fica sob o sinal do radical). Leia a observação seguinte para entender as razões pelas quais não uso o símbolo de radical neste trabalho.
Observação: Por deficiência da própria linguagem HTML, que até hoje não implementou o sinal de raiz n-ésima, usarei aqui Rn[a] para indicar a raiz n-ésima de a. Quando n=2, simplesmente indicarei a raiz de ordem 2 de um número inteiro a como R[a].
Dessa forma, b é a raiz n-ésima de a se, e somente se, a=bn, isto é:
b = Rn[a] <=> a = bn
Definição: A raiz quadrada (de ordem 2) de um número inteiro a é a operação que resulta em um outro número inteiro não negativo que elevado ao quadrado seja igual ao número a.
Observação importante: Não existe a raiz quadrada de um número inteiro negativo no conjunto dos números inteiros. A existência de um número cujo quadrado é igual a um número negativo só será estudada mais tarde no contexto dos números complexos.
Erro muito comum: Freqüentemente lemos em alguns materiais didáticos e até mesmo ocorre em algumas aulas aparecimento de:
R[9] = ±3
mas isto está errado. O certo é:
R[9] = +3
Observamos que não existe um número inteiro não negativo que multiplicado por ele mesmo resulte em um número negativo.
Definição: A raiz cúbica (de ordem 3) de um número inteiro a é a operação que resulta em um outro número inteiro que elevado ao cubo seja igual ao número a. Aqui não restringimos os nossos cálculos somente aos números não negativos.
Exemplos:
R3[8] = 2, pois 23 = 8.
R3[-8] = -2, pois (-2)3 = -8.
R3[27] = 3, pois 33 = 27.
R3[-27] = -3, pois (-3)3 = -27.
Observação: Obedecendo à regra dos sinais para a multiplicação de números inteiros, concluímos que:
Se o índice da raiz for par, não existe raiz de número inteiro negativo.
Se o índice da raiz for ímpar, é possível extrair a raiz de qualquer número inteiro.
Este texto foi retirado do site Cola na Web
Ao final da postagem tem uma videoaula.
Recomendo os seguintes links:
Como estudar para concursos públicos.
Conheça as características das principais bancas organizadoras de concursos públicos
Gostaria de lembrar também que tenho um livro de aventura que publiquei a versão final em e-book no Amazon, A fortaleza do Centro, dá uma olhadinha nele é muito legal.
Gostaria também de saber qual concurso você vai fazer, é só postar nos comentários
Abraços e bons estudos!
O produto cartesiano de dois conjuntos A e B são todos os pares ordenados (x, y), sendo que x pertence ao conjunto A e y pertence ao conjunto B.
Teoria dos conjuntos: as relações de pertinência, inclusão e igualdade
Relação de pertinência
Conceitos de conjuntos
Conjunto vazio: é um conjunto que não possui elementos. O conjunto vazio é representado por { } ou ![]() .
.
Subconjuntos: quando todos os elementos de um conjunto A qualquer pertencem a um outro conjunto B, diz-se, então, que A é um subconjunto de B, ou seja A![]() B. Observações:
B. Observações:
União de Conjuntos: dados os conjuntos A e B, define-se como união dos conjuntos A e B ao conjunto representado por ![]() , formado por todos os elementos pertencentes a A ou B, ou seja:
, formado por todos os elementos pertencentes a A ou B, ou seja: ![]()

Intersecção de Conjuntos:dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por ![]() , formado por todos os elementos pertencentes a A e B, simultaneam
, formado por todos os elementos pertencentes a A e B, simultaneam
Leia/ assista o vídeo até o final que resolverei 2 questões de concursos para você entender melhor
Os diagramas lógicos são usados para representar as proposições de um raciocínio lógico.
Se preferir, no vídeo abaixo tem a postagem em áudio e vídeo:
As questões de raciocínio lógico que usam os diagramas utilizam os quantificadores: