COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
![]() Diagramas lógicos – Diagrama de Venn
Diagramas lógicos – Diagrama de Venn
Leia/ assista o vídeo até o final que resolverei 2 questões de concursos para você entender melhor
Os diagramas lógicos são usados para representar as proposições de um raciocínio lógico.
Se preferir, no vídeo abaixo tem a postagem em áudio e vídeo:
As questões de raciocínio lógico que usam os diagramas utilizam os quantificadores:
Todo/ qualquer
Existe/ pelo menos um/ algum
Nenhum
Eles são muito utilizados em questões que todos fazem algo ou somente alguns fazem ou nenhum fazem ou fazem os dois.
Por exemplo uma reunião de condomínio que irão decidir sobre duas propostas (A e B). Eles podem concordar com as duas propostas (todo), com somente uma das propostas (alguns) ou com nenhuma das propostas (nenhum).
Com o diagrama de Venn fica mais fácil visualizar a situação:
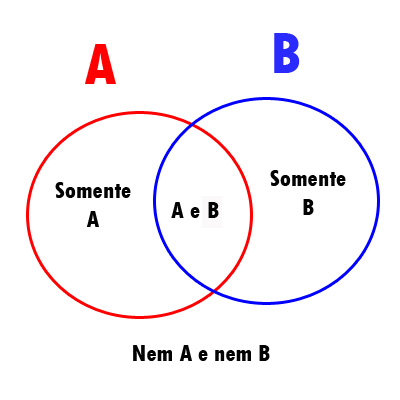
Vou explicar melhor cada um destes quantificadores:
Todo/ qualquer
Exemplo:
Todo mineiro gosta de queijo
Dois conjuntos: mineiro e gosta de queijo
João gosta de queijo
Diagrama:
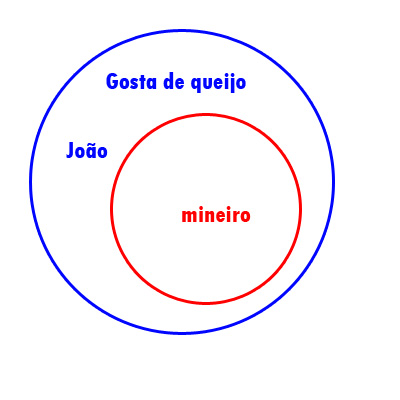
João faz parte do conjunto que gosta de queijo e não de mineiro, pois não se especificou se ele era mineiro ou não.
Não tem como afirmar que ele é mineiro, mas se especificar que ele é mineiro ele passaria para o outro conjunto (de mineiro).
Obs.: todos que estão no conjunto de mineiro (menor) faz parte do conjunto que gosta de queijo (maior), mas nem todos que estão no conjunto que gosta de queijo faz parte do conjunto de mineiro.
Existe/ pelo menos um/ algum
Exemplo:
Existem casas azuis
Dois conjuntos: o de casas e as de cor azul
Diagrama:
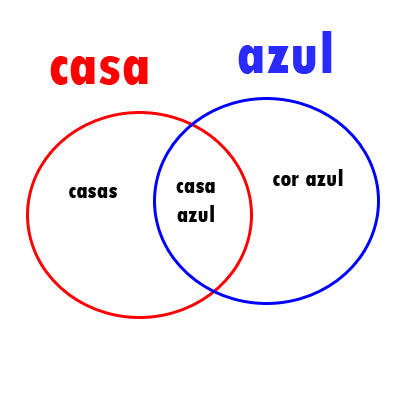
Eu sei que existem casas azuis, mas não posso garantir que não exista casa amarela ou verde. A intersecção dos dois contos garante que ali só tem casa azul.
Nenhum
Exemplo:
Nenhum estudante gosta de matemática
Diagrama:
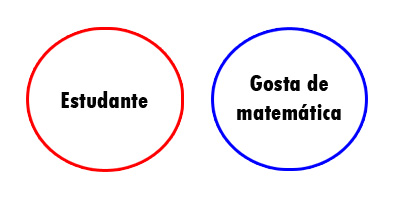
Se alguém gosta de matemática, ele não é estudante. Como os conjuntos não se conectam, não pode ter nenhum estudante que gosta de matemática.
Vamos analisar questões de concursos:
QUESTÃO 1
Ano: 2017 Banca: FGV Órgão: IBGE – Agente Censitário Municipal e Supervisor
Na assembleia de um condomínio, duas questões independentes foram colocadas em votação para aprovação. Dos 200 condôminos presentes, 125 votaram a favor da primeira questão, 110 votaram a favor da segunda questão e 45 votaram contra as duas questões.
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
Não houve votos em branco ou anulados.
O número de condôminos que votaram a favor das duas questões foi:
A 80;
B 75;
C 70;
D 65;
E 60.
Vamos usar o diagrama de Venn:

A pergunta é: Quantos condôminos votaram a favor das duas questões?
É muito simples:
200 (número de condôminos) – 45 (contra as duas) = 155
125 + 110 = 235 -155 = 80
RESPOSTA DA QUESTÃO 1 LETRA A
QUESTÃO 2
Ano: 2020 Banca: Quadrix Órgão: CREFONO-5° Região
Em uma academia de artes marciais que tem 288 alunos, 172 alunos praticam judô, 93 alunos praticam caratê e 25% dos alunos praticam ambas as modalidades.
Com base nessa situação hipotética, julgue o item.
É correto afirmar que 96 alunos não praticam nenhuma das duas modalidades.
Certo
Errado
Vamos resolver:
Diagrama de Venn
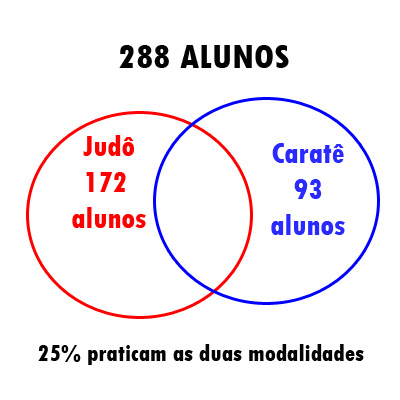
Vamos calcular 25% de 288 usando a regra de três simples:
288 ———– 100%
x————— 25%
100X = 288 x 25
100X = 7.200
X = 7.200/ 100
X = 72
O diagrama então fica assim:
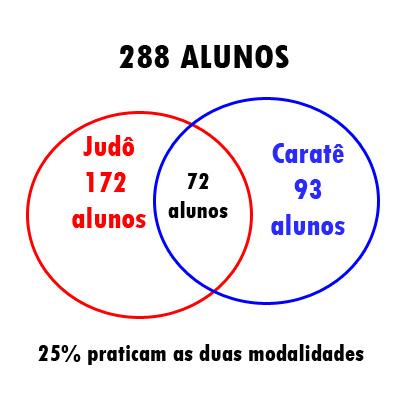
Agora muito importante o cálculo para não errar.
Agora sabendo que 72 alunos praticam as duas modalidades (intersecção), temos que saber quantos alunos praticam somente judô e caratê
Somente Judô: 172-72 = 100
Somente Caratê: 93 – 72 = 21
Vamos ao diagrama novamente:
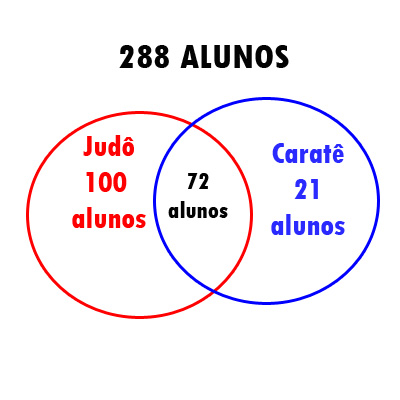
Agora é só calcular a união dos conjuntos e saberemos quantos praticam judô e caratê:
100 + 72 + 21 = 193 alunos praticam judô, caratê ou ambas.
Ele pergunta: É correto afirmar que 96 alunos não praticam nenhuma das duas modalidades.
Ele quer saber se tem 96 alunos que não praticam nenhuma das modalidades.
288 (número se alunos) – 193 (pratica pelo menos uma modalidade) = 95 , ou seja,
95 alunos não praticam nenhuma das duas modalidades e a afirmativa seria 96 então:
RESPOSTA DA QUESTÃO 2 ERRADO
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!



Obrigada!