COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
![]() Lógica de argumentação: analogias, inferências, deduções e conclusões
Lógica de argumentação: analogias, inferências, deduções e conclusões
Lógica de argumentação
Caso preferir, no vídeo abaixo tem esta postagem em áudio e vídeo
A lógica é como pensamos sobre o que sabemos, ou pelo menos, achamos que sabemos.
A argumentação é como usamos nosso raciocínio para tentar convencer alguém sobre algo que acreditamos estar correto. Esta argumentação para fazer sentido tem que estar baseado em informações disponíveis e preferencialmente sobre dados corretos.
A lógica de Argumentação é a proposição (premissas) do raciocínio lógico, ou seja, é baseada no que pode ser verdadeiro ou falso. Estas premissas têm uma explicação lógica para que possamos concluir algo.
Analogias
Este raciocínio faz comparações (semelhanças) entre casos conhecidos com desconhecidos.
Ela defende que existe alguma semelhança entre as proposições.
É a operação de estabelecer uma relação entre coisas em virtude de haver uma relação de semelhança entre elas.
Exemplos de raciocínio por analogia
Votar em branco é como deixar que outra pessoa escolha o sabor de seu refrigerante.
Se deixar de escolher o sabor do refrigerante e não gostar, não tem direito de reclamar.
Portanto, se votar em branco você não tem o direito de reclamar se o vencedor for um péssimo governante.
QUESTÃO DE CONCURSO
Banca: CESPE / CEBRASPE Órgão: FUNPRESP-EXE
Acerca dos argumentos racionais, julgue o item a seguir.
No diálogo a seguir, a resposta de B é fundamentada em um raciocínio por analogia.
A: O que eu faço para ser rico assim como você?
B: Como você sabe, eu não nasci rico. Eu alcancei o padrão de vida que tenho hoje trabalhando muito duro. Logo, você também conseguirá ter esse padrão de vida trabalhando muito duro.
Certo
Errado
Como vimos anteriormente o raciocínio por analogia faz comparações (semelhanças) entre casos conhecidos com desconhecidos.
No raciocínio por analogia, comparamos uma situação conhecida com uma desconhecida. A analogia é utilizada para “concluir” algo a partir de uma situação anterior. Agora analisando a questão, temos:
A: O que eu faço para ser rico assim como você?
B: Como você sabe, eu não nasci rico. Eu alcancei o padrão de vida que tenho hoje trabalhando muito duro.
Conclusão: Logo, você também conseguirá ter esse padrão de vida trabalhando muito duro.
Podemos ver que A não é rico e B não nasceu rico, mas B trabalhou muito duro para ser rico.
Usando o raciocínio por analogia chegamos a conclusão que se A trabalhar muito duro ficará rico como B.
RESPOSTA DA QUESTÃO: CORRETO
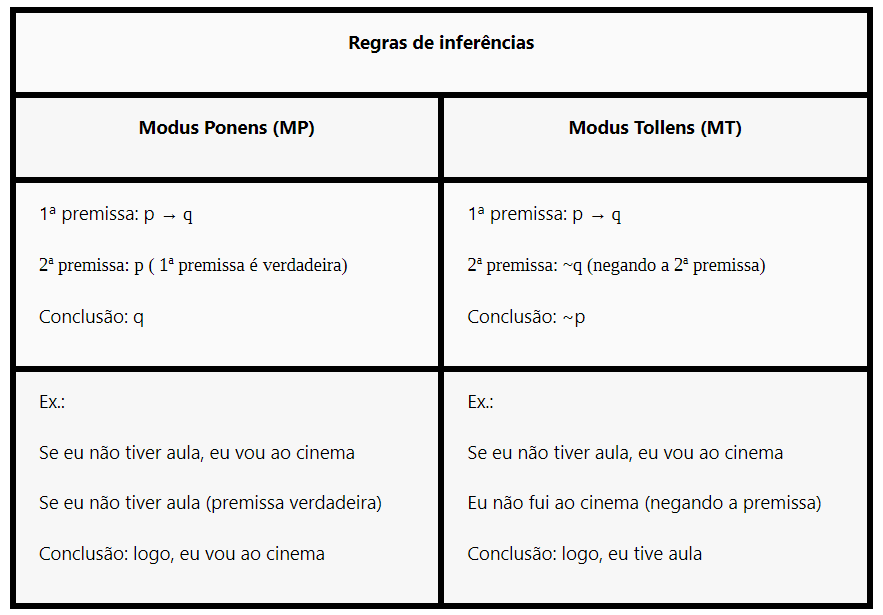
Inferências:
Inferência é a ação de inferir, ou seja, deduzir algo tirando uma conclusão. É um método que parte de uma ou mais premissas para achar novas proposições. Se a inferência for válida, significa que a nova proposição foi
Inferência: é o processo a partir de uma ou mais premissas se chegar a novas proposições. Quando a inferência é dada como válida, significa que a nova proposição pode ser utilizada em outras inferências.
Partindo de algumas hipóteses podemos inferir uma conclusão.
Silogismo: É fundamental para a inferência. É uma maneira de deduzir que é formada por duas premissas (proposições) e uma conclusão. Você chega a uma conclusão através da dedução de informações contidas nas duas premissas.
Nem todas as inferências oferecem conclusões verdadeiras.
Por exemplo: Podemos afirmar que todos as zebras são animais de quatro patas, mas não se pode inferir que todos os animais de quatro patas são zebras.
Quanto mais características tenha a premissa, maior é a chance de inferir corretamente.
Se perguntarem para você qual é o animal de quatro patas que tem listras, você poderá inferir com uma margem maior de acerto que pode ser uma zebra.
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
Deduções e conclusões
Existem dois processos de raciocínio:
Dedução
A dedução parte de uma certeza (uma premissa universal) para poder chegar a uma conclusão, ou seja, ela vai do todo a uma parte. Ela parte de algo abrangente para descobrir uma verdade particular. Ele tem mais segurança na conclusão por que usa premissas já aceita pelas pessoas.
Ex.:
Pedro é natural de Belo Horizonte
Belo Horizonte é uma cidade de Minas Gerais
Quem nasce em Minas Gerais é mineiro
Logo, Pedro é mineiro
Indução
É o oposto da dedução, pois parte de casos particulares, buscando semelhanças entre eles para se definir uma premissa universal, ou seja, ela vai da parte ao todo.
Ex.: O cão da Maria tem rabo
O cão do João tem rabo
O cão do Pedro tem rabo
Todo cão é um animal
Logo, todo animal tem rabo
Conclusão
É uma proposição que tem a resposta final da inferência que foi baseada nas premissas dadas.
Normalmente ela começa com as expressões logo, por isso, portanto….
QUESTÃO DE CONCURSO DE 2024
Ano: 2024 Banca: Instituto Consulplan Órgão: Prefeitura de Pitangueiras – SP Cargo: Topógrafo Nível: Médio
Disciplina: Raciocínio lógico Assunto: Lógica de argumentação
As amigas Noemi, Mírian e Priscila nasceram nas cidades de Belém, Belo Horizonte e Campos dos Goytacazes, mas não necessariamente nessa ordem. Considere que as seguintes afirmações sobre elas sejam verdadeiras:
• Noemi não nasceu em Campos dos Goytacazes;
• Mírian não nasceu em Belo Horizonte; e,
• Priscila não nasceu em Belo Horizonte e nem em Campos dos Goytacazes.
De acordo com o exposto, pode-se concluir que:
A Mírian nasceu em Belém.
B Noemi nasceu em Belém.
C Priscila nasceu em Belo Horizonte.
D Mírian nasceu em Campos dos Goytacazes.
Partindo que todas as afirmações sobre elas são verdadeiras:
Se Noemi não nasceu em Campos dos Goytacazes, então Noemi nasceu em Belém ou Belo Horizonte.
Se Mírian não nasceu em Belo Horizonte, então Mírian nasceu em Belém ou Campos dos Goytacazes.
Se Priscila não nasceu em Belo Horizonte e nem em Campos dos Goytacazes, então Priscila nasceu em Belém.
Logo
Priscila nasceu em Belém
Noemi nasceu em Belo Horizonte
Mírian nasceu em Campos dos Goytacazes
RESPOSTA DA QUESTÃO LETRA D
Mírian nasceu em Campos dos Goytacazes.
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!


