Sistema de medidas: decimais e não decimais Parte 2

Medidas de massa

A grandeza massa não é muito usual no dia a dia, mas muito comum quando nos deparamos com problemas de física. Unidade padrão: quilograma (kg)

Quilograma → 1 kg = 1000 g

Hectograma → 1 hg = 100 g

Decagrama → 1 dag = 10 g

Decigrama → 1 dg = 0,1 g

Centigrama → 1 cg = 0,01 g

Miligrama → 1 mg = 0,001 g

Dizemos 1.000 kg corresponde a 1 tonelada

1 t = 1.000 kg

Exemplos:

Converter 32 g em hg:

hg  ←  dag  ←  g

Deveremos deslocar a vírgula duas casas decimais para a esquerda.

32 g   =  0,32 hg

Converter 782 kg em toneladas:

Uma tonelada (1 t) equivale a 1.000 kg. Assim, deveremos dividir a quantidade de kg por 1.000, que é o mesmo que deslocar a vírgula três casas decimais à esquerda.

Logo, 782 kg = 0,782 t

 

Medidas de superfície ou área

Medidas de superfície ou área também está presente no nosso dia a dia. A unidade de medida padrão é: metro quadrado (m²)

1 km² → 1.000.000 m² = 106 m²

1 hm² → 10.000 m² = 104 m²

1 dam² →100 m² = 102 m²

1 dm² → 0,01 m² = 10-2 m²

1 cm² → 0,0001 m² = 10-4 m²

1 mm² → 0,000001 m² = 10-6 m²

 

Medidas agrárias

Os fazendeiros devem conhecer essa unidade de media muito bem e, aqui, você também vai entender. A unidade de medida padrão é: are (a)

1 a = 1 dam²

Hectare (ha) = 1 hm²

Centiare (ca) = 1 m²

Exemplos:

Converter 3,2 hm² em m²:

hm²  →  dam²  →  m²

3,2 hm² = 320 dam² = 32.000 m²

É o mesmo que deslocar a vírgula quatro casas decimais à direita, pois as unidades são quadradas.

Converter 48,6 dm² em m²:

m² ← dm²

Deveremos deslocar a vírgula duas casas decimais à esquerda.

48,6 dm² = 0,486 m²

Converter 21,7 ha em km²:

21,7 ha = 21,7 hm²

km²  ←  hm²

Deveremos deslocar a vírgula duas casas decimais à esquerda.

21,7 ha = 21,7 hm² = 0,217 km²

 

Medidas de volume

Quem nunca quis saber quanto cabe em uma caixa d’água, por exemplo. Para essa grandeza utilizamos a unidade de media padrão: metro cúbico (m³)

1 km³ = 109 m³

1 hm³ = 106 m³

1 dam³ = 103 m³

1 dm³ = 10-3 m³

1 cm³ = 10-6 m³

1 mm³ = 10-9 m³

Exemplos:

Converta 2.578 mm³ em dm³:

dm³ ← cm³ ← mm³

2.578 mm³ = 2,578 cm³ = 0,002.578 dm³

Na prática, é o mesmo que deslocar a vírgula três casas decimais para esquerda.

Converta 28,3 m³ em dm³:

m³ → dm³

Deveremos deslocar a vírgula três casas decimais para a direita.

28,3 m³ = 28.300 dm³

Fonte: Matemática básica

Sistema de medida: Não decimais

O sistema não decimal ou complexo compreende sistema de medida não ligado por relação decimal.

Exemplos:

Medidas de prazos ou intervalos de tempo, das medidas de ângulos e das grandezas referidas ao sistema inglês de pesos e medidas.

 

Medidas de Tempo

No Sistema Internacional, a unidade oficial de tempo é o segundo, cujo símbolo é s.

Além do segundo, as unidades de tempo mais usadas são o minuto, a hora, a semana, o mês, o ano, e o século. Temos que:

1 minuto =60 segundos;

1 hora = 60 minutos ;

1 hora = 3.600 segundos;

1 mês comercial = 30 dias;

1 ano comercial = 360 dias;

1 ano civil = 365 dias.

Também são unidades de tempo usuais:

– semana (7d);

– quinzena (15d);

– bimestre (2me);

– trimestre (3me);

– semestre (6me);

– lustro (5a);

– década (10a);

– século (100a).

 

Exemplo:

1.Transforme 789 dias em anos, meses e dias:

Verificaremos quantos anos cabem em 789 dias:

789dias : 360 = 2 anos e 69dias

em seguida verificaremos quantos meses cabem em 69 dias:

69dias : 30 = 2 meses e 09dias

Resposta: 2 anos, 2 meses e 9 dias.

2.Transforme 2,325 anos em: anos, meses e dias:

2,325 a = 2 a + 0,325 a

2 a + 0,325 . 12 meses

2 a + 3,9 meses

2 a + 3 meses + 0,9 meses

2 a + 3 meses + 0,9 . 30 dias

2 a + 3 meses + 27 dias

Resposta: 2 a + 3 meses + 27 dias

3.Efetue a adição abaixo indicada:

2h 47min 18 s + 3h 18min 51 s

 

5h 65min 69 s

Se 69 s = 1min + 9 s

Então fica:

5h 66min 09s

Se 66min = 1h + 6 min

Então fica:

6h 06min 09s

Resposta: 6h 06min 09s

4.Efetue a subtração abaixo indicada:

4h 26 min 12 s – 2h 35 min 45 s

Como 12 é menor que 45, tomamos 1 minuto (60 segundos) emprestado dos 26 minutos.

Ficará então:

4h 25 min 72 s – 2h 35 min 45 s

Como 25 minutos é menor que 35 minutos, tomamos 1h (60 minutos) emprestado de 4h.

Ficará finalmente:

3h 85 min 72 s – 2h 35 min 45 s

1h 50 min 27 s

Resposta: 1h 50 min 27 s

Fonte: Professor Luiz Bolinha

 

Medidas de ângulos

Os ângulos são medidos em graus, e as subunidades dos graus são os minutos, e as subunidades dos minutos são os segundos.

Desta forma:

1 grau equivale a 60 minutos; 1° = 60’

1 minuto equivale a 60 segundos; 1’ = 60”

Então podemos resolver utilizando a regra de 3, veja, se você tem por exemplo 5º (5 graus) e quer descobrir os minutos, faz assim:

1 está para 60 assim como 5 está para x (o valor que você quer descobrir).

1 = 60

5      x

Agora é só multiplicar o x por 1 e 60 por 5

x= 60.5

x= 300 minutos

Para transformar em segundos faz a mesma coisa. veja:

1 minuto está para 60 segundos assim como 300 minutos estão para x, veja:

1   = 60

300     x

x = 60. 300

x = 18.000 segundos.

Para descobrir o inverso faz o mesmo, é só colocar o x no lugar do que vc quer descobrir.

Fonte:Brainly

 

Operações com ângulos: adição, subtração, multiplicação e divisão

30°55’42” + 18°51’48”

30°55’42” +

18°51’48”

48°106’90” = decompondo 48° 60’46” 60” 30”

Ficando então: 49°47’30”

Outro exemplo:

Dado os ângulos de 6º 25’ 36” e 4º 40’ 30”, a soma entre eles é:

O resultado da soma é 10º 65’ 66”, porém podemos apresentar o resultado de uma outra forma. Acompanhe a demonstração:

No ângulo de medida 10º 65’ 66”, temos que 65’ = 60’ + 5’ = 1º + 5’ e 66” = 60” + 6” = 1’ + 6”. Dessa forma, 10º 65’ 66” = 11º 6’ 6”.

 

Subtração

Dados os ângulos 54º 16’ 32” e 27º 18’ 40”, a subtração entre eles é:

 

 

 

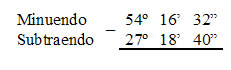
Observe que existem valores no minuendo que são menores dos que os valores do subtraendo, quando isso acontece na subtração temos que tirar do valor da esquerda completando o que está menor.

Ao retirarmos 1’ de 16’ ficaremos com 15’, sendo que 1’ = 60” o qual deve ser somado a 32” resultando em 92”.

 

 

 

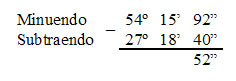
Agora devemos retirar 1º de 54º que será igual à 53º, considerando que 1º = 60’, temos 60’ + 15’ = 75’. Portanto:

 

 

 

 

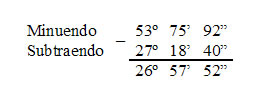
O resultado da subtração é igual a 26º 57’ 52”.

Fonte: Brasil escola

 

DIVISÃO DE ÂNGULOS

 

 

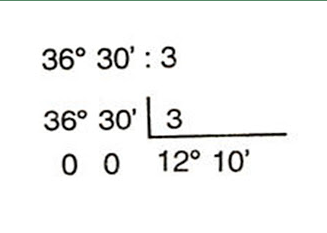
• Juros e desconto simples (juro, capital, tempo, taxa e montante).

•  Funções do 1º e 2º graus: problemas.

• Sistema monetário brasileiro: problemas.