COMBO CARREIRA BANCÁRIA COM 9 APOSTILAS POR APENAS R$ 28,90 CLIQUE AQUI!!
![]() Continuando nossa série de artigos/ vídeos sobre estruturas lógicas, aqui falaremos aqui sobre conectivos lógicos.
Continuando nossa série de artigos/ vídeos sobre estruturas lógicas, aqui falaremos aqui sobre conectivos lógicos.
Caso preferir, no vídeo abaixo tem esta postagem em áudio e vídeo
Estruturas lógicas:
O assunto estruturas lógicas se divide em:
Proposições lógicas (lógica proposicional)
Tautologia, Contradição e Contingência
Conectivos lógicos
O conectivo lógico é um símbolo ou palavra que usamos para conectar duas ou mais proposições para que elas sejam válidas, de modo que a proposição composta formada dependa apenas das proposições que a originou. Por causa dos conectivos conseguimos dar um valor lógico para esta proposição formada.
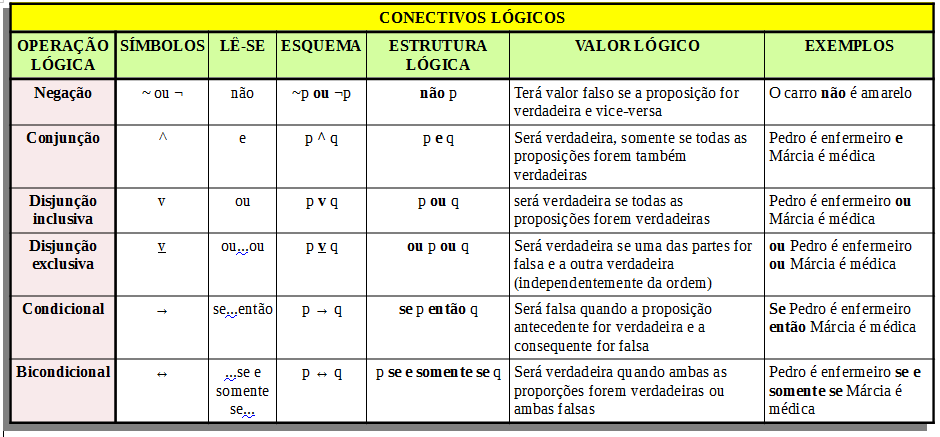
Negação (Conectivo ~ ou ¬)
COMBO CNU - 2024 COM 8 APOSTILAS POR APENAS R$ 29,90 - SAIA NA FRENTE!!
Conectivo: “não”
Símbolo: ~ ou ¬
Esquema: ~p ou ¬p (não p)
Proposição p: O carro é amarelo
Proposição ~p: O carro não é amarelo
ou ~p : Não é verdade que o carro é amarelo
ou ~p : É falso que o carro é amarelo
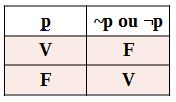
Tabela verdade:
O carro é amarelo (p)
Uma proposição: 2¹ = 2
Conjunção (conectivo “e”)
Disjunção Exclusiva:
COMBO INSS COM 8 APOSTILAS POR APENAS R$ 26,90 COMECE A SE PREPARAR!!!



Muito bom!
Oi Bianca, obrigado pelo comentário
EXCELENTE, VLW.
Obrigada!