Leitura de gráficos de barras ou colunas e tabelas simples
Fica muito mais fácil você entender uma situação através de gráficos e tabelas. Você verá eles no nosso dia a dia, como em jornais, revistas e na internet.
As informações ficam mais claras e organizadas facilitando a sua interpretação.
Medidas de tempo, massa e temperatura
Medidas de Tempo
No Sistema Internacional, a unidade básica de tempo é o segundo, cujo símbolo é s.
Unidade de medida não decimal
Problemas do campo aditivo (adição e subtração) e multiplicativo (multiplicação e divisão)
Caso preferir, no vídeo abaixo tem esta postagem em áudio e vídeo
Campo aditivo (adição e subtração)
Sistema de numeração decimal
É um sistema de numeração que utiliza dez unidades (algarismos), na qual a partir dela se formam os outros números.
Os algarismos são: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
Problemas envolvendo função de 1º grau
As funções são utilizadas na representação cotidiana de situações que envolvam valores constantes e variáveis, sempre colocando um valor em função do outro. Por exemplo, ao abastecermos o carro no posto de gasolina, o preço a ser pago depende da quantidade de litros de combustível colocada no tanque. Abordaremos as situações problemas ligadas às equações do 1º grau, respeitando a lei de formação f(x) = ax + b, com a ≠ 0.
VOLUME
Segundo o Sistema Internacional de medidas (SI) a unidade padrão de volume é o metro cúbico (m3). 1 m3 equivale a 1.000 litros.
Cada unidade de medida tem equivalência de 1000 vezes multiplicando (unidade maior para uma menor) ou dividindo (unidade menor para uma maior)
Exemplos:
Quanto é o equivalente de 5 m3 em cm3 ?
Saindo de uma unidade maior para uma menor então multiplicamos
5 x 1.000 (dm3) x 1.000 (cm3) = 5.000.000 cm3
Quanto é o equivalente de 5.000.000 cm3 em m3 ?
Saindo de uma unidade menor para uma maior então dividimos
5.000.000 cm3 : 1.000 (dm3) : 1000 (m3) = 5 m3
Se quiser simplificar o cálculo é só deslocar a vírgula em três casas para a direita (maior para a menor unidade) ou esquerda (menor para a maior unidade).
Ângulos
É a medida de abertura entre duas semirretas com um ponto em comum chamado de origem.
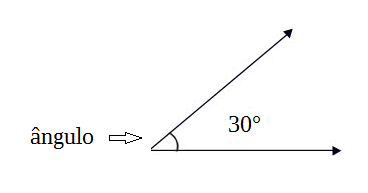
Classificação dos ângulos quanto à sua medida:
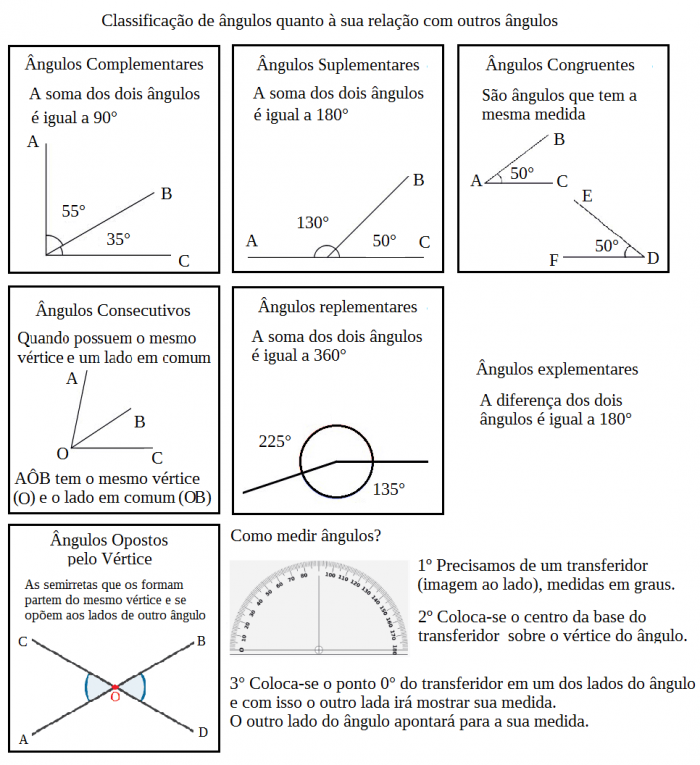
Classificação de ângulos quanto à sua relação com outros ângulos
TEOREMA DE PITÁGORAS
Em um triângulo retângulo, o lado maior, recebe o nome de Hipotenusa. Este lado sempre estará oposto ao ângulo reto. Os outros dois lados, recebem o nome de Cateto.
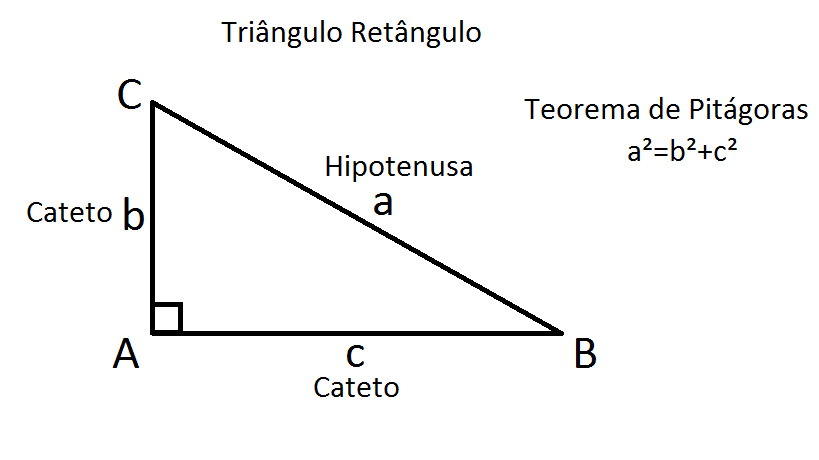
Teorema de Pitágoras:
“Em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos”.
QUESTÃO DE CONCURSOS:
Ano: 2016 Banca: IDHTEC Órgão: Prefeitura de Barra de Guabiraba – PE
O teorema de Pitágoras tem sido utilizado até hoje e com muita aplicabilidade a diversas situações cotidianas. Por exemplo, se uma escada de 5 m está encostada no topo em uma parede de 4 m, dá pra descobrir que o pé dessa escada está afastado 3 m da parede. Imagine agora que essa escada possua 13 m e que o pé dela esteja afastado 5 m da parede. Qual a altura do topo da parede onde a escada está encostada?
A 12 m
B 11 m
C 10 m
D 9 m
E 8 m
Resolução:
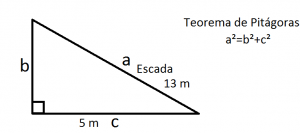Escada(a): 13 m
Afastamento(c): 5 m
Altura da parede(b): ?
Teorema de Pitágoras: a²=b²+c²
13²=b²+5²
169=b²+25
b²=169-25
b²=144
b=12
RESPOSTA DA QUESTÃO LETRA A
Números fracionários
Os números fracionários são aqueles representados por frações. No momento de realizar as operações, é preciso rever algumas dicas práticas.
ADIÇÃO E SUBTRAÇÃO
Sistema Price (Sistema Francês)
Todas as prestações (pagamentos) são iguais.
Uso comum: Financiamentos em geral de bens de consumo.
Cálculo: O cálculo da prestação P é o produto do valor financiado Vf=300.000,00 pelo coeficiente K dado pela fórmula
Sistemas de medida de tempo
No sistema de medidas internacional temos as unidades de tempo.
As mais comuns são:
Segundo, minuto e horas
Este tempo também pode medir dias, semanas ou mês.
Vamos começar a calcular a partir dos segundo, pois apesar de termos décimos (1/10 ou 0,1 s), centésimos (1/100 ou 0,01s) e milésimos de segundo (1/1000 ou 0,001s), ela não costuma ser utilizada no nosso dia a dia.
Operações com números racionais
Adição e Subtração
Para simplificar a escrita, transformamos a adição e subtração em somas algébricas. Eliminamos os parenteses e escrevemos os números um ao lado do outro, da mesma forma como fazemos com os números inteiros.
Exemplo 1: Qual é a soma:
Operações com números racionais
Adição e Subtração
Para simplificar a escrita, transformamos a adição e subtração em somas algébricas. Eliminamos os parenteses e escrevemos os números um ao lado do outro, da mesma forma como fazemos com os números inteiros.
Exemplo 1: Qual é a soma:
Relação de inclusão
Exemplo 01
Considere os conjuntos abaixo:
A = {1, 2, 3}
B = {1, 2, 3, 4, 5}
temos:
1 ∈ A e 1 ∈ B
2 ∈ A e 2 ∈ B
3 ∈ A e 3 ∈ B
Perceba que, todos os elementos do conjunto A também pertencem ao conjunto B, então podemos afirmar que A está contido em B, podendo ser indicado da seguinte maneira: A ⊂ B. E se A ⊂ B, podemos também dizer que B contém A, podendo ser indicado da seguinte maneira: B ⊃ A.
Exemplo 02
Agora considere os seguintes conjuntos abaixo:
A = {0, 1, 2, 3}
B = {1, 2, 3, 4}
temos:
0 ∈ A e 0 ∉ B
1 ∈ A e 1 ∈ B
2 ∈ A e 2 ∈ B
3 ∈ A e 3 ∈ B
Operações com conjuntos
União de conjuntos: AUB é formado por todos os elementos que pertence ao conjunto A e conjunto B
Tratamento da informação – média aritmética simples
A média aritmética simples é a mais comum e muito utilizada no nosso dia a dia.
A média aritmética simples é obtida na seguinte forma:
Resolução de situações-problema, envolvendo: adição, subtração, multiplicação, divisão, potenciação ou radiciação com números racionais, nas suas representações fracionária ou decimal
Números Racionais
Interseção dos conjuntos: Naturais, Inteiros e Racionais.
Os números decimais são aqueles números que podem ser escritos na forma de fração.
