Ano: 2009 Banca: FGV Órgão: SAD-PE
Observe as figuras abaixo:
Ano: 2009 Banca: FGV Órgão: SAD-PE
Observe as figuras abaixo:
Ano: 2017 Banca: CPCON Órgão: Prefeitura de Major Sales – RN
![]() Medidas de comprimento, área, volume, massa e tempo
Medidas de comprimento, área, volume, massa e tempo
Medida de comprimento
A unidade de medida padrão: metro (m)
Quilômetros → 1 km = 1000 m
Hectômetro → 1 hm = 100 m
Decâmetro → 1 dam = 10 m
Decímetro → 1 dm = 0,1 m
Centímetro → 1 cm = 0,01 m
Respostas e explicações
CASO QUEIRA VER AS PERGUNTAS E O CONTEÚDO TEÓRICO CLIQUE AQUI!
QUESTÃO 1
Como o modelo do exemplo é completamente escuro, você só pode construir uma “figura completamente escura”. Portanto, a resposta será a marcada com a letra “b”, porque as outras figuras têm setores brancos.
![]() Conjunção (conectivo “e”)
Conjunção (conectivo “e”)
Conectivo “e” é denominado conjunção e seu símbolo é o acento circunflexo “^”
O esquema é p ^ q (p e q)
Será verdadeira somente se todas as proposições forem verdadeiras
Ex.:
Solução:
1.Nega-se a primeira parte (~p) = João não é médico;
2.Nega-se a segunda parte (~q) = Pedro não é dentista;
3.Troca-se E por OU, e o resultado final será o seguinte:
JOÃO NÃO É MÉDICO OU PEDRO NÃO É DENTISTA.
Relação de inclusão
Exemplo 01
Considere os conjuntos abaixo:
A = {1, 2, 3}
B = {1, 2, 3, 4, 5}
temos:
1 ∈ A e 1 ∈ B
2 ∈ A e 2 ∈ B
3 ∈ A e 3 ∈ B
Perceba que, todos os elementos do conjunto A também pertencem ao conjunto B, então podemos afirmar que A está contido em B, podendo ser indicado da seguinte maneira: A ⊂ B. E se A ⊂ B, podemos também dizer que B contém A, podendo ser indicado da seguinte maneira: B ⊃ A.
Exemplo 02
Agora considere os seguintes conjuntos abaixo:
A = {0, 1, 2, 3}
B = {1, 2, 3, 4}
temos:
0 ∈ A e 0 ∉ B
1 ∈ A e 1 ∈ B
2 ∈ A e 2 ∈ B
3 ∈ A e 3 ∈ B
![]() Raciocínio lógico envolvendo problemas aritméticos, geométricos e matriciais.
Raciocínio lógico envolvendo problemas aritméticos, geométricos e matriciais.
Além dos conhecimentos de raciocínio lógico que você deve ter como tabela verdade, diagramas de Venn, conectivos, estruturas lógicas dentre outros, você deve ter conhecimento sobre aritmética (números), geometria e matrizes.
Faremos então várias questões de concurso que envolve estes conhecimentos.
Raciocínio lógico: Problemas aritméticos
Para resolver problemas aritméticos de raciocínio lógico é necessário o conhecimento de aritmética, ou seja, operações com números, ou seja, operações de adição, subtração, multiplicação, divisão, frações, múltiplos e divisores e números pares e ímpares.
![]() Operações com conjuntos
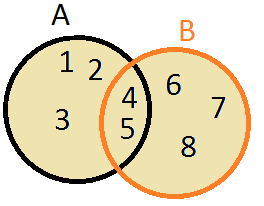
Operações com conjuntos
União de conjuntos: AUB é formado por todos os elementos que pertence ao conjunto A e conjunto B
![]() Argumentação lógica
Argumentação lógica
Também conhecida como Raciocínio Lógico: Lógica de argumentação
A lógica é como pensamos sobre o que sabemos ou achamos que sabemos. Ela é usada para podermos trabalhar nosso raciocínio. Poderíamos dividi-la em duas formas:
![]() Raciocínio sequencial
Raciocínio sequencial
O raciocínio sequencial pode ser conhecido de diversas maneiras como: Lógica sequencial ou sequência lógica.
Geralmente é uma sequência de figuras, letras, números ou palavras.
Para podermos ter uma sequência lógica para efetuarmos um raciocínio é necessário pelo menos Três elementos
A melhor maneira de entender o raciocínio sequencial é resolvendo questões.
Raciocínio Lógico: Orientação espacial e temporal
Esta parte do Raciocínio lógico é muito interessante, pois dentro do conhecimento geral adquirido na escola e se lermos atentamente a questão buscando o padrão que foi desenvolvido a questão, você conseguirá resolver, pois é apenas uma questão de lógica certo?
O raciocínio lógico espacial ou orientação espacial envolvem figuras, dados e palitos. O raciocínio espacial é uma habilidade importante que gera conceitos e soluções para problemas que surgem em áreas como arquitetura, engenharia, ciências, matemática, arte, jogos, e também no cotidiano. É preciso um bom raciocínio espacial para navegar pelas ruas, usar mapas, resolver quebra-cabeças ou jogar sinuca, decorar a casa, estudar geometria e física, ou simplesmente decidir se é possível fazer um sofá passar pela porta.
Entendimento da estrutura lógica de relações arbitrárias entre pessoas, lugares, objetos ou eventos fictícios
Bom antes de colocar a matéria algumas explicações devem ser colocadas, para que você entenda o que estão pedindo. No Brasil há uma mania de mudarem as coisas só para complicar, não sei se é a elite intelectual que quer aparecer ou se é mania de grandeza. fizeram a mesma coisa com o Enem e agora vira e mexe fazem em concursos. Mudam os termos e o aluno que se vire; colocam termos genéricos que força o concurseiro a estudar um monte de matérias desnecessárias e como são genéricos os examinadores fazem do jeito que quiserem.
 Compreensão e elaboração da lógica das situações por meio de raciocínio matemático.
Compreensão e elaboração da lógica das situações por meio de raciocínio matemático.
Raciocínio matemático:
O raciocínio lógico-matemático auxilia na resolução de problemas lógicos, envolvendo sequências de figuras, palavras ou números; conjuntos; frações; razões e proporções; porcentagens, álgebra, leitura de tabelas e gráficos, Probabilidade e Geometria.
Você praticamente tem que saber matemática de forma geral, mas o importante é saber interpretar o que está pedido (texto) para sistema matemático.