Conceitos de raciocínio lógico
Raciocínio lógico é um processo de estruturação do pensamento de acordo com as normas da lógica que permite chegar a uma determinada conclusão ou resolver um problema.
Um raciocínio lógico requer consciência e capacidade de organização do pensamento. Existem diferentes tipos de raciocínio lógico, como o dedutivo e o indutivo.
Raciocínio Indutivo
Raciocínio Lógico Dedutivo
A dedução é uma inferência que parte do universal para o mais particular. Assim considera-se que um raciocínio lógico é dedutivo quando, de uma ou mais premissas, se conclui uma proposição que é conclusão lógica da(s) premissa(s). A dedução é um raciocínio de tipo mediato, sendo o silogismo uma das suas formas clássicas. Iniciaremos com a compreensão das sequências lógicas, onde devemos deduzir, ou até induzir, qual a lei de formação das figuras, letras, símbolos ou números, a partir da observação dos termos dados.
Neste item do edital a banca pediu várias matérias, então para facilitar a localização coloquei todas aqui com links para as postagens:
Conectivos (conectivos lógicos)
Validade de argumento (argumentos válidos)
Dica: Para você que não esta encontrando o conteúdo que precisa ou prefere estudar por apostilas dá uma olhada no site Apostilas Opção, lá eles tem praticamente todas as apostilas atualizadas de todos os concursos abertos. Caso queira saber por que indico as Apostilas opção clique aqui!
Para vocês entenderem lógica argumentativa sobre afirmações e negações, precisam aprender algumas regrinhas.
1° João é corinthiano
2° Pedro é flamengista
Duas afirmações que também são chamadas de proposições
A primeira chamaremos de proposição P e a segunda de Q.
Posso também fazer a negação delas, ou seja uma afirmação negativa, representado por este símbolo (~ ).
Conceito
Um argumento pode ser definido como uma afirmação acompanhada de justificativa (argumento retórico) ou como uma justaposição de duas afirmações opostas, argumento e contra-argumento (argumento dialético)
Na lógica e na filosofia um argumento é um conjunto de uma ou mais sentenças declarativas, também conhecidas como proposições, ou ainda, premissas, acompanhadas de uma outra frase declarativa conhecida como conclusão.
Argumento dedutivo
Em um argumento dedutivo (válido) o valor-verdade da conclusão é uma consequência lógica necessária das premissas que a antecedem, ou seja, sendo verdadeiras as premissas segue-se que necessariamente será verdadeira a conclusão. Caso alguma(s) premissa(s) não seja(m) verdadeira(s), uma conclusão verdadeira será apenas uma contingência. Também será contingente a verdade de uma conclusão num argumento dedutivo inválido, ou seja, um argumento em que mesmo a veracidade integral das premissas não garante, necessariamente, uma conclusão verdadeira.
Compreensão do processo lógico que, a partir de um conjunto de hipóteses, conduz, de forma válida, a conclusões determinadas.
Pesquisei este assunto em várias páginas de referências, páginas de cursos, apostilas de raciocínio lógico e inclusive em fórum onde participava professores de Raciocínio Lógico e ninguém sabe com 100% de segurança o que engloba esta matéria.
Dentre tudo que pesquisei o conteúdo que teve mais consenso entre os professores é que estas matérias são a mesma coisa de Conceitos Básicos de raciocínio lógico ( como é pedido em outros concursos) só que de uma maneira mais bonita, contemporânea e “chique”. Então relacionei as matérias abaixo de que você deve estudar:
Propriedades Comutativa, Distributiva e Leis de De Morgan
Equivalência Lógica
Portanto, dizemos que duas proposições são equivalentes se, e somente se, o resultado de suas tabelas-verdade for idêntico.
Bom antes de colocar a matéria algumas explicações devem ser colocadas, para que você entenda o que estão pedindo. No Brasil há uma mania de mudarem as coisas só para complicar, não sei se é a elite intelectual que quer aparecer ou se é mania de grandeza. fizeram a mesma coisa com o Enem e agora vira e mexe fazem em concursos. Mudam os termos e o aluno que se vire; colocam termos genéricos que força o concurseiro ter que estudar um monte de matérias desnecessárias e como são genéricos os examinadores fazem do jeito que quiserem.
Pesquisei este assunto : Compreensão e elaboração da lógica das situações por meio de: raciocínio verbal,raciocínio matemático, raciocínio sequencial, orientação espacial e temporal, formação de conceitos, discriminação de elementos.
Proposições associadas a uma condicional: Recíproca, Contrária e Contrapositiva
Proposição recíproca de p —> q : q —> p
Proposição contrária de p —> q : ~p —> ~q
Proposição contrapositiva de p —> q : ~q —> ~p
Equivalências: p —> q <==> ~q —> ~p e q —> p <==> ~p —> ~q
| O QUE VOCÊ VAI ENCONTRAR AQUI |
|
Dado que cada proposição pode ser, simultaneamente, classificada em função da qualidade e da quantidade. São quatro tipos de proposições categóricas.
Equivalência Lógica
Caro aluno, estudamos as implicações lógicas e foi enfatizado que o ponto fundamental da implicação lógica (P implica uma proposição Q, indica-se por P ⇒ Q), é que sempre que temos um antecedente verdadeiro, teremos um consequente verdadeiro também. Está lembrado? Vimos também que se uma proposição P implica uma proposição Q, não garante dizer o caminho inverso, isto é, que Q também implica P. Neste capítulo trataremos de ver as situações que envolvem o caminho de ida e de volta quando consideramos as implicações. Estas implicações são denominadas de equivalências lógicas.
Conceito:
Diz-se que uma proposição composta P é logicamente equivalente a uma proposição composta Q (indica-se pela notação P ⇔ Q – o símbolo ⇔ é uma forma abreviada de dizer que duas proposições são logicamente equivalentes) quando, as tabelas verdade destas duas proposições compostas são idênticas. De outra forma, podemos dizer que as proposições P e Q são equivalentes, se a bicondicional P
Q for uma tautologia.
E para iniciar este estudo das equivalências lógicas, considere as seguintes proposições:
Na primeira proposição temos uma dupla negação, logo se “não vi ninguém” (dupla negação), então “vi alguém”.(afirmação) Podemos concluir que estas proposições são equivalentes. Desta forma, tenha cuidado ao usar “não vi ninguém” com o sentido de pessoa alguma foi vista. Isto é lógico para você?
Podemos construir uma tabela-verdade e colocar todos os valores lógicos possíveis. Vamos ver como ficam?
Para esta construção, considere p: vi alguém
Perceba que a última coluna da tabela-verdade é a bicondicional e ela é sempre verdadeira, e portanto tautológica.
Os valores lógicos de p e ~(~p) são idênticos. Desta forma, podemos concluir que estas proposições são logicamente equivalentes. E também são equivalentes as proposições compostas p→~(~p) e ~(~p) → p, e esta equivalência expressa a lei da dupla negação.
Podemos indicar estas equivalências da seguinte forma:
Vamos trabalhar esta noção de equivalência por meio de alguns outros exemplos:
1º Exemplo: Veja as seguintes sentenças:
Parece intuitivo que sejam logicamente equivalentes?
É verdade, pois possuem o mesmo “conteúdo lógico”.
Vamos analisar melhor esta situação, utilizando agora os conceitos da Lógica Matemática. E para isto, considere as proposições:
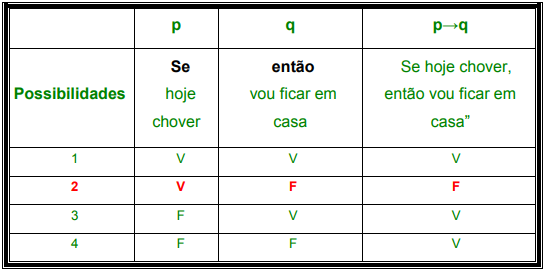
p: Hoje é sábado.
q: Hoje é dia de pegar um cineminha.
Vamos verificar como ficam os possíveis valores lógicos na tabela-verdade para cada sentença dada inicialmente:
Você lembra que a condicional p→q será logicamente falsa apenas quando o antecedente (p) é verdadeiro e o consequente (q) é falso? Veja a possibilidade 2. (2ª linha da tabela)
Vamos agora para a segunda sentença. E para isto, considere as proposições p e q e suas negações ~p e ~q
Se você observar atentamente as tabelas, facilmente perceberá que as últimas colunas das tabelas, que são das proposições condicionais (p→q) e (~q→~p), são idênticas. Desta forma, podemos concluir que há aqui uma equivalência lógica. Assim sendo, as sentenças I e II, são equivalentes:
I -Se hoje é sábado, então hoje é dia de pegar um cineminha. (p→q)
II -Se hoje não é dia de pegar um cineminha, então hoje não é sábado. (~q→~p)
Simbolicamente representamos esta equivalência da seguinte maneira:
(p→q) ⇔ (~q→~p) (Esta equivalência é denominada de Contrapositiva da condicional dada.)
Releia o conceito inicial de equivalência lógica e observe que:
(p→q) corresponde a proposição composta
P (~q→~p) corresponde a proposição composta Q
É importante que você valorize aquilo que temos estudado dentro da Lógica Matemática, pois certamente a fundamentação teórica é importante para o entendimento de situações, inclusive as do nosso cotidiano.
Vamos ver mais alguns exemplos de equivalência entre proposições (P ⇔ Q). Nosso objetivo é que você entenda a construção das tabelas-verdade como um instrumento importante de verificação das equivalências lógicas, pois sempre que os valores lógicos das proposições P e Q forem idênticos, elas serão equivalentes.
2º Exemplo: Vamos para o seguinte enunciado:
Verificar a equivalência das proposições a seguir:
p ∧ q ⇔ q ∧ p .
observação:
p ∧ q corresponde a proposição composta P.
q ∧ p corresponde a proposição composta Q.
Vamos recorrer à tabela-verdade e colocar os valores lógicos de cada proposição.
Perceba que neste caso, as colunas das proposições “p ∧ q” e “q ∧ p” são idênticas, logo são equivalentes, e sendo equivalentes, a coluna da bicondicional tem sempre valores lógicos verdadeiros, e portanto a bicondicional é considerada tautológica.
Uma aplicação bastante interessante de equivalência lógica entre as proposições condicionais e as proposições com o conectivo “ou” (disjunção) é:
3º Exemplo: Neste 3º exemplo, verificaremos uma transformação de uma proposição condicional em proposição com o conectivo “ou” (disjunção), pois são equivalentes. (p→q) ⇔ (~p v q ).
Achou estranha esta equivalência? Podemos compreendê-la, utilizando a tabela-verdade. Para que não fiquemos trabalhando apenas com letras e para que não vejamos este tópico com estranheza e distância, vamos buscar uma solução para o enunciado abaixo:
Enunciado: Transforme, através da equivalência por disjunção, a proposição condicional “Se estudo, passo no teste”.
Veja que inicialmente temos as seguintes proposições:
p: estudo
q: passo no teste
A proposição dada no enunciado é a proposição composta que podemos representar matematicamente por p→q e a pedida é ( ~p v q ).
Veja, se utilizarmos a equivalência citada anteriormente (p→q) ⇔ ( ~p v q), podemos escrever:
A proposição condicional “Se estudo, passo no teste” (p→q) é logicamente equivalente a proposição com o conectivo “ou” (disjunção) “Não estudo ou passo no teste” (~p v q)
Vamos verificar esta equivalência, por meio da tabela-verdade.
Observe que os valores lógicos das proposições “p→q” e “~p v q” são idênticos.
Resumindo
Vale destacar que toda equivalência é uma implicação lógica por natureza. Diferentemente, a implicação não se trata necessariamente de uma equivalência lógica. Podemos então dizer que toda equivalência é uma implicação lógica, mas nem toda implicação é uma equivalência lógica.
Fonte: Apostila disponibilizada na internet pela Uniban
E você, qual o concurso você vai fazer? Deixe um comentário para mim, pois posso fazer postagens direcionadas para ele e te ajudar mais. Aproveita também para inscrever seu e-mail para receber conteúdos todos os dias.
Dica: Para você que não esta encontrando o conteúdo que precisa ou prefere estudar por apostilas dá uma olhada no site Apostilas Opção, lá eles tem praticamente todas as apostilas atualizadas de todos os concursos abertos. Caso queira saber por que indico as Apostilas Opção clique aqui!
Resolução de problemas envolvendo frações, conjuntos, porcentagens, sequências (com números, com figuras, de palavras).
2º exemplo: p ⇒ q → p Vamos verificar esta implicação.
Atenção: A intenção aqui, caro aluno, é que você perceba que o ponto fundamental da implicação lógica ( P implica uma proposição Q, indica-se por P ⇒ Q), é que sempre que temos um antecedente verdadeiro, teremos um consequente verdadeiro também.
Vamos verificar se “p” de fato implica a proposição composta “q → p” (p ⇒ q → p)
Atenção: A proposição condicional q→p (lê-se: “se q então p”) é uma proposição composta que só admite valor lógico falso no caso em que a proposição q é verdadeira e a proposição p é falsa, sendo verdade nas demais situações. (veja a 3ª coluna da tabela seguinte)
p ⇒ q → p, pois o condicional p→ (q→p) é tautológica.
Perceba que quando p é verdadeira (1ª e 2ª colunas), q→p é verdadeira também, logo dizemos que p implica a proposição composta q → p. (p ⇒ q → p)
Vamos agora mostrar as implicações no 3º e 4º exemplos.
3º exemplo: p Λ q ⇒ p v q
Caro aluno, não se assuste com o tamanho das tabelas-verdade. Você deve organizar as colunas, e para iniciar, atribua todos os valores lógicos possíveis para as proposições simples p e q. (são quatro situações; isto é, são quatro linhas).
Para compreender a tabela acima, você deverá retomar as operações da conjunção e disjunção, além, obviamente, da condicional.
Observe que na 3ª coluna (p Λ q), temos uma conjunção, e que ela é logicamente verdadeira apenas quando as proposições simples p e q são ambas verdadeiras, e logicamente falsas nas demais situações.
Observe que na 4ª coluna (p v q), temos uma disjunção, e que ela é logicamente falsa apenas quando as proposições simples p e q são ambas falsas, e logicamente verdadeiras nas demais situações. Até aqui, tudo bem? Se ficou claro, então vamos entender melhor a 5ª coluna.
Na 5ª e última coluna, temos a condicional (p Λ q) → (p v q) logicamente verdadeira para todas as situações, pois a condicional só é falsa quando o antecedente é verdadeiro e o consequente falso.
Podemos verificar a implicação p Λ q ⇒ p v q, por meio da condicional (p Λ q) → (p v q), pois, neste exemplo, ela é sempre verdadeira e, portanto, tautológica. Você também pode verificar a implicação dada observando que quando a proposição p Λ q é verdadeira, temos que p v q, também, é verdadeira (1ª linha). Logo, está verificada a implicação dada.
4º exemplo: p ⇒ p v q
Neste 4º exemplo , também verificamos a implicação p ⇒ p v q , pois a condicional p → (p v q) é tautológica.
Observe que quando a proposição p é verdadeira, temos que p v q, também, é verdadeira (1ª e 2ª linhas). Logo, está verificada a implicação dada.
Observação O fato de dizer que uma proposição P implica uma proposição Q, não garante dizer o caminho inverso, isto é, que Q também implica P.
Abaixo estudaremos as situações que envolvem o caminho de ida e de volta quando consideramos as implicações. Neste caso chamaremos de equivalências lógicas.
Equivalência Lógica
Continua na parte 4
Em qual das possibilidades a situação foi descumprida?
Não é difícil concluir que na possibilidade 2, a situação foi descumprida. Você deve estar se perguntando sobre a possibilidade 3. Afinal, se não fez sol, como viajaram para a praia? Parece estranho, não? Na verdade, temos que tomar um certo cuidado, o pai só disse o que fariam se fizesse sol, mas não disse o que fariam se não fizesse sol. Esta é razão da condicional na linha 3 ser logicamente verdadeira. Temos que ter muita atenção, especialmente nesta parte. Esta é a parte que as pessoas, em geral, apresentam mais dificuldades de compreensão. Por este motivo vamos discutir um pouco mais sobre o assunto.
Utilizamos com frequência sentenças condicionais, como: “Se hoje chover, então vou ficar em casa”. Vamos ver as quatro possibilidades para esta situação:
Caro aluno, é importantíssimo que você aprenda que na lógica matemática não nos preocupamos com qualquer relação de causa e efeito entre o antecedente e o consequente de uma implicação. O que há é uma relação entre os valores lógicos. Neste exemplo, ficou claro para você que na possibilidade 2, a situação foi descumprida; isto é, “choveu e não fiquei em casa” ? É provável que você tenha dúvidas com relação à possibilidade 3. Afinal, se não choveu, como fiquei em casa? Voltamos a dizer, sendo o antecedente (p) logicamente falso, não importa o valor lógico do consequente (q), pois o valor lógico da condicional será sempre verdadeiro!
Desta forma, releia o conceito:
A proposição condicional “se p então q” é uma proposição composta que só admite valor lógico falso no caso em que a proposição p é verdadeira e a proposição q é falsa, sendo verdade nas demais situações.
E qual é a importância da implicação?
O conceito de implicação é essencial para os diversos campos do conhecimento. Como exemplo, podemos citar as implicações lógicas de um discurso que remete a explicação ou demonstração de argumentos, e isto não é restrito à Matemática. É comum aparecerem declarações do tipo: “Sempre que isto ocorre, e, é verdadeiro, implica que aquilo também é verdadeiro”. Pense nas diversas áreas, tais como: Medicina, Direito, Engenharia, Educação, Propaganda e Marketing, Processamento de Dados e tantas outras áreas, que utilizam inúmeras implicações. Enfim vivemos imersos em um mundo de implicações lógicas! Pense a este respeito.
A implicação é muito importante na linguagem matemática porque aparece sistematicamente nos teoremas que constituem as teorias matemáticas. Um teorema é uma proposição do tipo p ⇒ q, onde p é uma proposição verdadeira na teoria em questão. Demonstrar um teorema não é mais do que provar que a proposição p ⇒ q é verdadeira e sendo p verdadeira, por hipótese, implica dizer que q é também verdadeira. Num teorema é comum chamarmos a proposição p de hipótese, é o antecedente da implicação p ⇒q. A proposição q, que é o consequente da implicação, é denominada de tese. As demonstrações de teoremas são essenciais para o desenvolvimento de habilidades e competências relacionadas à experimentação, observação e percepção, realização de conjecturas, desenvolvimento de argumentações convincentes, entre outras.
O símbolo P⇒ Q (P implica Q) representa a implicação lógica. Observe neste conceito que aparecem dois símbolos matemáticos → e ⇒. Vamos diferenciá-los?
Diferenciação dos símbolos → e ⇒
Você já deve ter se familiarizado com o primeiro (símbolo →), pois fizemos uso dele em vários exemplos envolvendo a operação lógica da condicional em que podíamos fazer um julgamento (verdadeiro ou falso), já o segundo (símbolo ⇒) passaremos a ver agora com mais detalhes. Tenha sempre em mente que o símbolo ⇒ representa uma implicação, cuja condicional será sempre tautológica, isto é, será sempre logicamente verdadeira. Vamos agora ver alguns exemplos e verificar a implicação lógica indicada em cada caso.
Exemplos:
Vamos comprovar isto para o 1ª exemplo dado. p ^ q ⇒ p
Considere a situação:
p: Marina Silva vencerá as eleições para a Presidência do Brasil.
q: A taxa de desemprego cairá nos próximos três anos.
p ^ q: Marina Silva vencerá as eleições para a Presidência do Brasil e a taxa de desemprego cairá nos próximos três anos.
Vamos agora verificar como ficam os possíveis valores lógicos das proposições:
Relembrando: Você está lembrado que a proposição composta da conjunção p ^ q (p e q) somente será verdadeira quando as proposições p e q forem verdadeiras.
Perceba que quando p ^ q é verdadeira (1ª possibilidade, veja o quadro acima), p é verdadeira também, logo dizemos que p ^ q implica p e, tem a seguinte notação: p ^ q ⇒ p. E mais, se você fizer a condicional (p ^ q) → p, ela será sempre verdadeira, ou seja uma tautologia.
2º exemplo: p ⇒ q → p Vamos verificar esta implicação.
Continua na parte 3
Inferências:
Inferência é a ação de inferir, ou seja, deduzir algo tirando uma conclusão. É um método que parte de uma ou mais premissas para achar novas proposições. Se a inferência for válida, significa que a nova proposição foi
Inferência: é o processo a partir de uma ou mais premissas se chegar a novas proposições. Quando a inferência é dada como válida, significa que a nova proposição pode ser utilizada em outras inferências.
Então mais curioso ainda você perguntou: “Se os números racionais são todos aqueles que podem ser expressos na forma de fração, então existem aqueles que não podem ser expressos desta forma?”
Exatamente, estes números pertencem ao conjunto dos números irracionais. Provavelmente os mais conhecidos deles sejam o número PI ( ), o número de Euler (
) e a raiz quadrada de dois (
). Se você se dispuser a calcular tal raiz, passará o restante da sua existência e jamais conseguirá fazê-lo, isto porque tal número possui infinitas casas decimais e diferentemente das dízimas, elas não são periódicas, não podendo ser expressas na forma de uma fração. Esta é uma característica dos números irracionais.
